Ультимативный гайд по структурам данных и алгоритмам на Python. Часть 2: стеки, очереди и связанные списки

Привет! Это вторая часть из цикла статей "Ультимативный гайд по структурам данных и алгоритмам на Python" 🧠. В первой части мы заложили фундамент, разобравшись с базовыми инструментами, которые Python предоставляет "из коробки". Мы увидели их сильные стороны и "подводные камни" производительности. Теперь пора двигаться дальше и осваивать более продвинутые концепции и инструменты!

Эффективные стеки и очереди

"А что, списки не подходит?" 🤔

# Анти-пример: Очередь на list
print("Демонстрация проблемы с list.pop(0):")
queue_list = ['A', 'B', 'C', 'D']
print(f" Исходная очередь: {queue_list}, id: {id(queue_list)}")

# Извлекаем первый элемент (Dequeue) - O(n)!
first_item = queue_list.pop(0)
print(f" Извлекли: '{first_item}'")
print(f" Очередь после pop(0): {queue_list}, id: {id(queue_list)}")
# Заметьте, что 'B', 'C', 'D' сдвинулись на индексы 0, 1, 2!
# ID списка тот же, но внутреннее содержимое перестроено.

deque: решение проблемы ✨

from collections import deque

# Создаем deque
d = deque(['b', 'c', 'd'])
print(f"Исходный deque: {d}")

# Работаем с правым концом (как list)
d.append('e')      # O(1)
print(f"После append('e'): {d}")
item_right = d.pop() # O(1)
print(f"После pop(): {item_right=}, deque: {d}")

# Работаем с левым концом (быстро, в отличие от list!)
d.appendleft('a') # O(1)
print(f"После appendleft('a'): {d}")
item_left = d.popleft() # O(1)
print(f"После popleft(): {item_left=}, deque: {d}")

Вывод: `deque` — это не полная замена списков. Это специализированный инструмент, который очень хорошо, когда вам нужны быстрые (O(1)) операции добавления/удаления с обоих концов последовательности.

Пример использования deque для стеков (LIFO)

from collections import deque

# Используем deque как стек для истории команд
command_history = deque()
print("Симуляция работы с текстовым редактором:")

# Пользователь выполняет действия (push через append)
action1 = "Набрать текст: 'Привет'"
command_history.append(action1)
print(f" -> Выполнено: '{action1}', Стек: {command_history}")

action2 = "Сделать текст жирным"
command_history.append(action2)
print(f" -> Выполнено: '{action2}', Стек: {command_history}")

action3 = "Добавить смайлик 😎"
command_history.append(action3)
print(f" -> Выполнено: '{action3}', Стек: {command_history}")

# Пользователь нажимает "Отмена" (pop)
print("\nНажата кнопка 'Отмена'...")
if command_history: # Проверяем, что стек не пуст
    last_action = command_history.pop() # O(1)
    print(f" <- Отменено действие: '{last_action}'")
    print(f"    Осталось в стеке: {command_history}")
else:
    print("Нет действий для отмены.")

# Еще раз "Отмена"
print("\nНажата кнопка 'Отмена'...")
if command_history:
    last_action = command_history.pop() # O(1)
    print(f" <- Отменено действие: '{last_action}'")
    print(f"    Осталось в стеке: {command_history}")
else:
    print("Нет действий для отмены.")

Пример использования deque для очередей (FIFO)

from collections import deque
import time
import random

# Используем deque как очередь для заданий на печать
printer_queue = deque()

# Моделируем поступление заданий (Enqueue через append)
print("\n--- Моделирование очереди печати ---")
print("Поступают задания:")
for i in range(1, 6): # 5 заданий
    job_name = f"Document_{i}.pdf"
    printer_queue.append(job_name) # O(1)
    print(f"  [+] Поступило: '{job_name}'. Очередь: {list(printer_queue)}") # list() для наглядности
    time.sleep(random.uniform(0.2, 0.5)) # Имитация паузы между заданиями

# Моделируем работу принтера (Dequeue через popleft)
print("\nПринтер начинает обработку:")
while printer_queue: # Пока очередь не пуста
    current_job = printer_queue.popleft() # O(1) - Быстрое извлечение!
    print(f"  [*] Печатается: '{current_job}'...")
    processing_time = random.uniform(0.5, 1.0) # Имитация времени печати
    time.sleep(processing_time)
    print(f"  [✓] Готово: '{current_job}' (за {processing_time:.2f} сек). Осталось в очереди: {len(printer_queue)}")

print("\n--- Очередь печати пуста! Принтер свободен. ---")

Связанные списки: зачем понимать узлы и ссылки?🔗

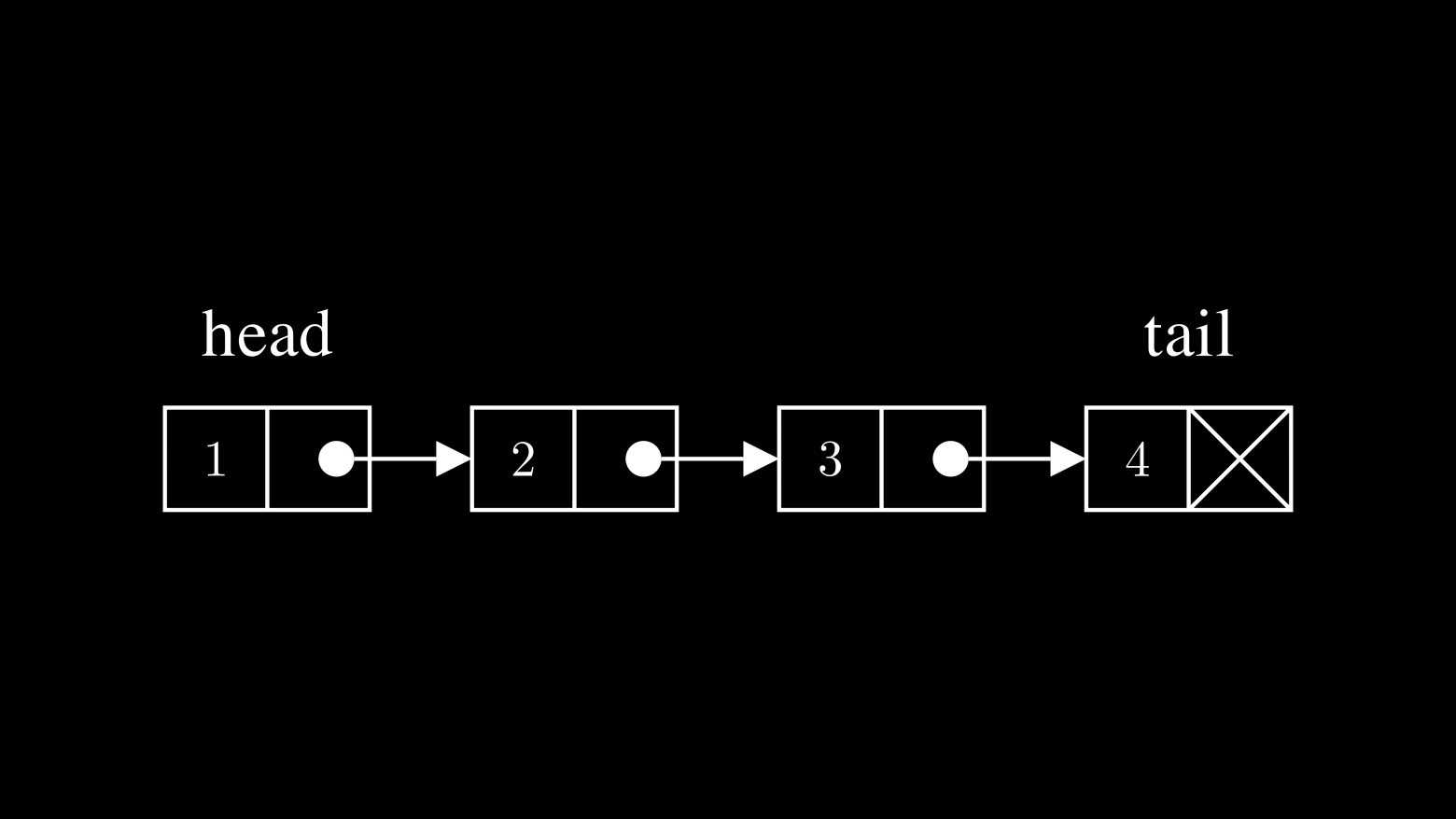
Ключевая идея: узлы не обязаны лежать в памяти рядом друг с другом. Они могут быть разбросаны где угодно. Единственное, что связывает их в последовательность — это цепочка ссылок `next`, идущая от `head` до `None`.

"Зачем мне это в Python, если есть list и deque?" 🤔

Ценность понимания связанных списков✨

Итог: связанные списки — это не столько инструмент для ежедневного использования, сколько важнейший элемент образования. Это как знать основы алгебры, чтобы понимать высшую математику.

Базовая реализация в Python

class Node:
    """
    Представляет узел (звено) односвязного списка.
    Хранит данные и ссылку на следующий узел.
    """
    def __init__(self, data=None):
        self.data = data  # Данные, которые хранит узел
        self.next = None  # Ссылка на следующий узел, по умолчанию None

    def __repr__(self):
        """Возвращает строковое представление данных узла.
           Удобно при печати всего списка.
        """
        return str(self.data)

class LinkedList:
    """
    Представляет сам односвязный список.
    Хранит ссылку на голову (head) и предоставляет базовые операции.
    """
    def __init__(self, nodes_data=None):
        """
        Инициализирует связанный список.
        Может принимать итерируемый объект (например, list, tuple)
        для создания узлов списка при инициализации.
        """
        self.head = None # Изначально список пуст, головы нет

        if nodes_data is not None:
            # Пытаемся создать список из переданных данных
            try:
                # Получаем итератор, чтобы работать с любым итерируемым типом
                iterator = iter(nodes_data)
                # Создаем голову из первого элемента
                first_node_data = next(iterator)
                self.head = Node(first_node_data)
                current_node = self.head

                # Добавляем и связываем остальные элементы
                for elem_data in iterator:
                    current_node.next = Node(elem_data)
                    current_node = current_node.next # Переходим к только что созданному узлу
            except StopIteration:
                # Исходный итератор был пуст, self.head останется None
                pass
            except TypeError:
                # Переданный объект неитерируемый
                print("Ошибка: Для инициализации LinkedList нужны итерируемые данные.")
                self.head = None # Сбрасываем на всякий случай

    def __repr__(self):
        """
        Возвращает человекочитаемое строковое представление всего списка.
        Формат: data1 -> data2 -> ... -> None
        """
        nodes_repr = []
        current_node = self.head
        while current_node is not None:
            # Добавляем представление данных текущего узла (используя Node.__repr__)
            nodes_repr.append(str(current_node))
            current_node = current_node.next # Переходим к следующему узлу

        nodes_repr.append("None") # Явно показываем конец списка
        return " -> ".join(nodes_repr)

# 1. Создание пустого списка
empty_llist = LinkedList()
print(f"Пустой список: {empty_llist}")

# 2. Создание узлов и ручное связывание
node1 = Node('A')
node2 = Node('B')
node3 = Node('C')

# Связываем их: A -> B -> C -> None
node1.next = node2
node2.next = node3

# Создаем список и назначаем голову
manual_llist = LinkedList()
manual_llist.head = node1
print(f"Список, связанный вручную: {manual_llist}")

# 3. Создание списка из итерируемого объекта (списка Python)
auto_llist = LinkedList(['Раз', 'Два', 'Три'])
print(f"Список, созданный из list: {auto_llist}")

# 4. Создание из другого итератора (например, range)
range_llist = LinkedList(range(5))
print(f"Список, созданный из range(5): {range_llist}")

# 5. Пример с пустым итератором
empty_init_llist = LinkedList([])
print(f"Список, созданный из []: {empty_init_llist}")

Обход связанного списка: шаг за шагом по цепи 🕵️‍♂️

class Node:
    """ Узел связанного списка (без изменений) """
    def __init__(self, data=None):
        self.data = data
        self.next = None
    def __repr__(self):
        return str(self.data)

class LinkedList:
    """ Сам связанный список """
    def __init__(self, nodes_data=None):
        self.head = None
        # ... (код инициализации из предыдущего шага без изменений) ...
        if nodes_data is not None:
            try:
                iterator = iter(nodes_data)
                first_node_data = next(iterator)
                self.head = Node(first_node_data)
                current_node = self.head
                for elem_data in iterator:
                    current_node.next = Node(elem_data)
                    current_node = current_node.next
            except StopIteration: pass
            except TypeError:
                print("Ошибка: Для инициализации LinkedList нужны итерируемые данные.")
                self.head = None

    def __repr__(self):
        """ Представление списка (без изменений) """
        nodes_repr = []
        current_node = self.head
        while current_node is not None:
            nodes_repr.append(str(current_node))
            current_node = current_node.next
        nodes_repr.append("None")
        return " -> ".join(nodes_repr)

    # !!! ВОТ ОН, НАШ ИТЕРАТОР !!!
    def __iter__(self):
        """
        Позволяет итерироваться по данным узлов списка
        с помощью стандартного цикла for.
        """
        current = self.head  # Начинаем с головы
        while current is not None:
            yield current.data # Возвращаем данные текущего узла
            current = current.next # Переходим к следующему

# Создадим плейлист
my_playlist = LinkedList(["The Beatles", "Queen", "Led Zeppelin", "Pink Floyd"])
print(f"Мой плейлист: {my_playlist}")

print("\nВоспроизводим треки (итерация с помощью for):")
for track in my_playlist: # Теперь это работает благодаря __iter__!
    print(f"  🎶 Сейчас играет: {track}")

# Мы можем использовать и другие конструкции, ожидающие итерируемый объект:
playlist_list = list(my_playlist) # Преобразовать в обычный список Python
print(f"\nПлейлист как Python list: {playlist_list}")

playlist_tuple = tuple(my_playlist) # Преобразовать в кортеж
print(f"Плейлист как tuple: {playlist_tuple}")

# Посчитаем длину "питоничным" способом (хотя это O(n) под капотом!)
length = len(playlist_list) # len() работает со списком, полученным из итератора
# Или можно было бы реализовать __len__ в LinkedList, который бы делал обход
print(f"Количество треков: {length}")

Мой плейлист: The Beatles -> Queen -> Led Zeppelin -> Pink Floyd -> None

Воспроизводим треки (итерация с помощью for):
  🎶 Сейчас играет: The Beatles
  🎶 Сейчас играет: Queen
  🎶 Сейчас играет: Led Zeppelin
  🎶 Сейчас играет: Pink Floyd

Плейлист как Python list: ['The Beatles', 'Queen', 'Led Zeppelin', 'Pink Floyd']
Плейлист как tuple: ('The Beatles', 'Queen', 'Led Zeppelin', 'Pink Floyd')
Количество треков: 4

Итог: Хотя вы не будете писать `class LinkedList` каждый день, работая на Python, потраченное время на понимание их концепции окупится сторицей. Это знание расширяет ваш кругозор, помогает глубже понять другие структуры данных и алгоритмы, а также подготовит вас к каверзным вопросам на собеседованиях. Считайте это необходимой теоретической базой для любого серьезного разработчика.

Заключение: знание о новых инструментах 🛠️🧠

Ключевой вывод: Не существует "идеальной" структуры данных на все случаи жизни. Выбор всегда зависит от конкретной задачи и требований к производительности для разных операций. `deque` бьет `list` на операциях с начала, но проигрывает в доступе по индексу. Связанный список (теоретически) выигрывает при вставке в середину, но ужасен для поиска. Понимание этих компромиссов и внутреннего устройства — ключ к написанию по-настоящему эффективного кода.