Итак, финишная прямая нашего гайда!🚀 В прошлой части мы покорили иерархические структуры — деревья. Но что если связи между объектами не такие строгие? Что если отношения могут быть разнонаправленными, образовывать циклы, а "корня" как такового и вовсе нет?
Здесь на сцену выходят графы (Graphs) — самая общая и гибкая структура данных для моделирования связей между объектами. Социальные сети (люди и дружба), карты дорог (города и пути), интернет (страницы и ссылки), зависимости в проектах — всё это графы. По сути, почти любая система, где есть сущности и отношения между ними, может быть представлена графом. Деревья — это лишь частный, более строгий случай графа.
Сегодня мы разберемся, какими они бывают, научимся представлять их в коде Python (матрицей или списком смежности) и освоим базовые алгоритмы их обхода — BFS и DFS, которые являются ключом к решению множества графовых задач.
Здесь на сцену выходят графы (Graphs) — самая общая и гибкая структура данных для моделирования связей между объектами. Социальные сети (люди и дружба), карты дорог (города и пути), интернет (страницы и ссылки), зависимости в проектах — всё это графы. По сути, почти любая система, где есть сущности и отношения между ними, может быть представлена графом. Деревья — это лишь частный, более строгий случай графа.
Сегодня мы разберемся, какими они бывают, научимся представлять их в коде Python (матрицей или списком смежности) и освоим базовые алгоритмы их обхода — BFS и DFS, которые являются ключом к решению множества графовых задач.
Весь маршрут нашего гайда:
Начнем с основ: что же такое граф с точки зрения computer science?
Графы, их вершины и рёбра
Если деревья — это строгие иерархии, то графы — это про свободу связей. Они представляют собой универсальную математическую структуру для моделирования отношений между объектами.
Формально, граф G — это пара (V, E), где:
- V — это множество вершин (Vertices), также называемых узлами (Nodes). Вершины представляют собой сами объекты или сущности в нашей системе (например, люди в соцсети, города на карте, веб-страницы, задачи в проекте, атомы в молекуле).
- E — это множество рёбер (Edges), также называемых дугами (Arcs) или связями (Links). Рёбра представляют собой связи или отношения между парами вершин (например, дружба между людьми, дорога между городами, гиперссылка между страницами, зависимость между задачами, химическая связь между атомами).
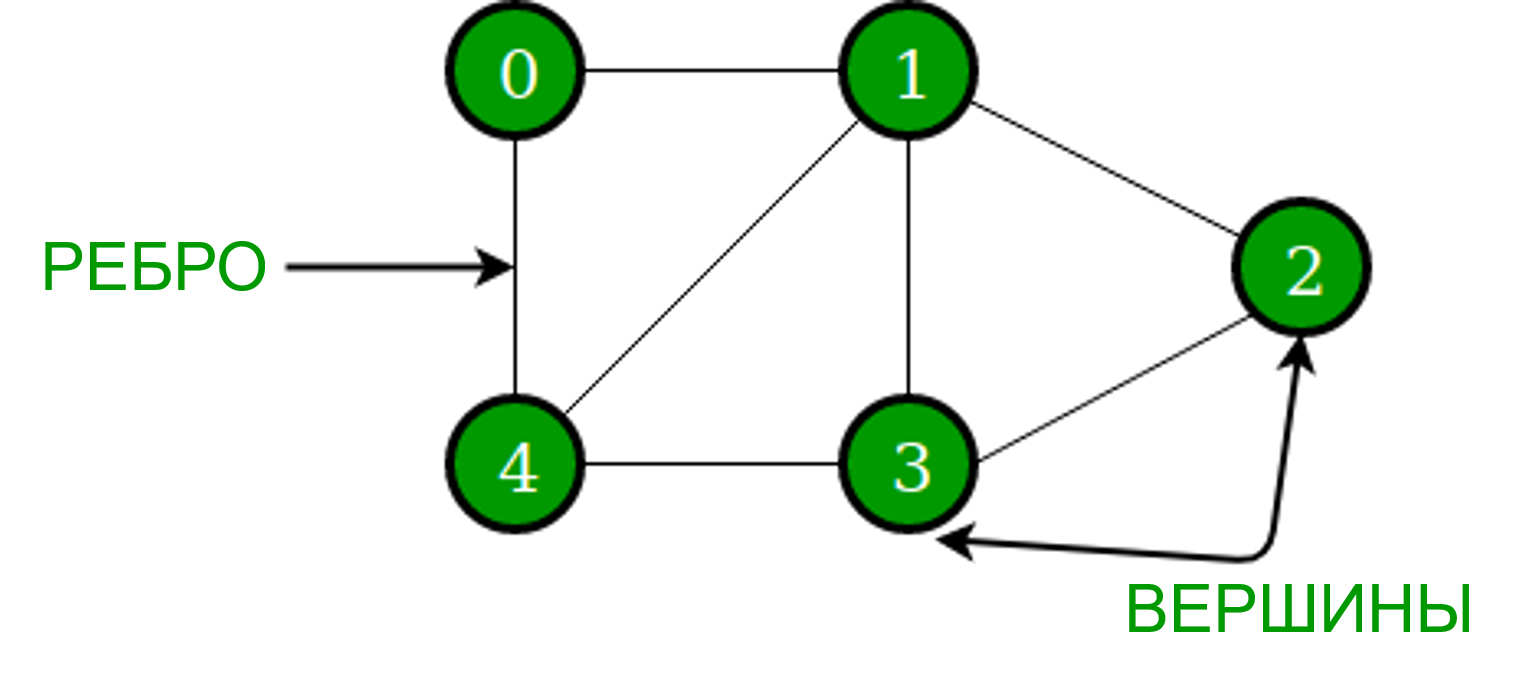
Эта простая концепция — вершины и рёбра — позволяет описать невероятное количество реальных и абстрактных систем. Но чтобы эффективно работать с графами, нужно понимать их разновидности, так как разные типы графов требуют разных подходов к представлению и обработке.
Классификация графов
Графы могут сильно различаться по своим свойствам, что влияет на их представление и алгоритмы. Вот основные типы:
По направлению рёбер
- Неориентированные (Undirected): Рёбра представляют двустороннюю связь. Если есть ребро между A и B, то можно пройти от A к B и от B к A. Пример: дружба в соцсети (обычно взаимна), карта дорог (если дорога не односторонняя). Ребро — неупорядоченная пара {A, B}.
- Ориентированные (Directed, Орграф): Рёбра имеют направление (A → B). Это односторонняя связь: можно пройти от A к B, но не обязательно наоборот. Пример: подписка в соцсети, веб-ссылки, зависимости задач (задача А должна быть сделана перед Б). Ребро — упорядоченная пара (A, B).
По весу рёбер
- Невзвешенные (Unweighted): Все рёбра "равноценны", важен лишь сам факт наличия связи.
- Взвешенные (Weighted): Каждому ребру присвоен вес (число), обозначающий, например, расстояние, стоимость, время прохождения, пропускную способность.
По наличию циклов
- Ациклические (Acyclic): Графы, в которых нет циклов. Цикл — это путь, начинающийся и заканчивающийся в одной и той же вершине.
- Циклические (Cyclic): Графы, содержащие хотя бы один цикл.
Ориентированные Ациклические Графы (DAG — Directed Acyclic Graph) — очень важный тип орграфов без циклов, часто используемый для моделирования зависимостей, расписаний, этапов выполнения.
Пример неориентированного взвешенного графа:
(0) --10-- (1)
| \ / |
5 6 4 | <-- Ребро(0,1) вес 10, Ребро(0,4) вес 5, ...
| \ / | (Цифры в скобках - вершины)
(4) --8-- (2)
\ /
7 3
\ /
(3)Понимание этих характеристик помогает выбрать правильный способ представления графа в коде и подходящие алгоритмы для работы с ним.
Как закодировать граф?
Просто знать вершины и рёбра недостаточно. Нам нужен эффективный способ хранить структуру графа в памяти, чтобы алгоритмы (обходы, поиск пути и т.д.) могли быстро получать нужную информацию (например, "есть ли ребро между A и B?" или "какие соседи у вершины C?").
Существует два классических способа представления графов 👇🏻
Матрица смежности (Adjacency Matrix)
Идея: Создать двумерный массив (матрицу) размером V x V, где V — количество вершин. Строки и столбцы матрицы соответствуют вершинам (обычно пронумерованным от 0 до V-1).
Значение в ячейке `matrix[i][j]` равно:
- 1 (или весу ребра для взвешенного графа), если существует ребро из вершины `i` в вершину `j`.
- 0 (или `None`, `float('inf')` для взвешенных, если ребра нет), если ребра `i -> j` нет.
- Для неориентированного графа матрица будет симметричной (`matrix[i][j] == matrix[j][i]`).
- Для ориентированного графа она может быть несимметричной.
Пример неориентированного невзвешенного графа, 5 вершин 0-4), с такими рёбрами: (0, 1), (0, 4), (1, 2), (1, 3), (1, 4), (2, 3), (3, 4)
num_vertices = 5
# Инициализация матрицы нулями
adj_matrix = [[0] * num_vertices for _ in range(num_vertices)]
edges = [(0, 1), (0, 4), (1, 2), (1, 3), (1, 4), (2, 3), (3, 4)]
for u, v in edges:
adj_matrix[u][v] = 1
adj_matrix[v][u] = 1 # Симметрично для неориентированного
print("Матрица смежности:")
for row in adj_matrix:
print(row)
# Пример вывода:
# [0, 1, 0, 0, 1]
# [1, 0, 1, 1, 1]
# [0, 1, 0, 1, 0]
# [0, 1, 1, 0, 1]
# [1, 1, 0, 1, 0]
# Проверка ребра (1, 4): O(1)
print(f"\nРебро (1, 4) существует? {'Да' if adj_matrix[1][4] == 1 else 'Нет'}")Плюсы и минусы матрицы смежности:
- 👍🏻: Очень быстрая проверка наличия ребра между `i` и `j` — просто посмотреть `matrix[i][j]`. Сложность O(1).
- 👍🏻: Удобно для плотных графов (где количество рёбер E близко к V²).
- 👎🏻: Требует много памяти — O(V²), даже если рёбер мало (для разреженных графов это очень неэффективно).
- 👎🏻: Добавление/удаление вершины требует перестройки всей матрицы (O(V²)).
- 👎🏻: Получение всех соседей вершины `i` требует просмотра всей i-й строки (O(V)).
Список смежности (Adjacency List)
Идея: Вместо хранения информации обо всех возможных парах вершин, для каждой вершины хранить только список (или множество) её непосредственных соседей — вершин, с которыми она соединена ребром.
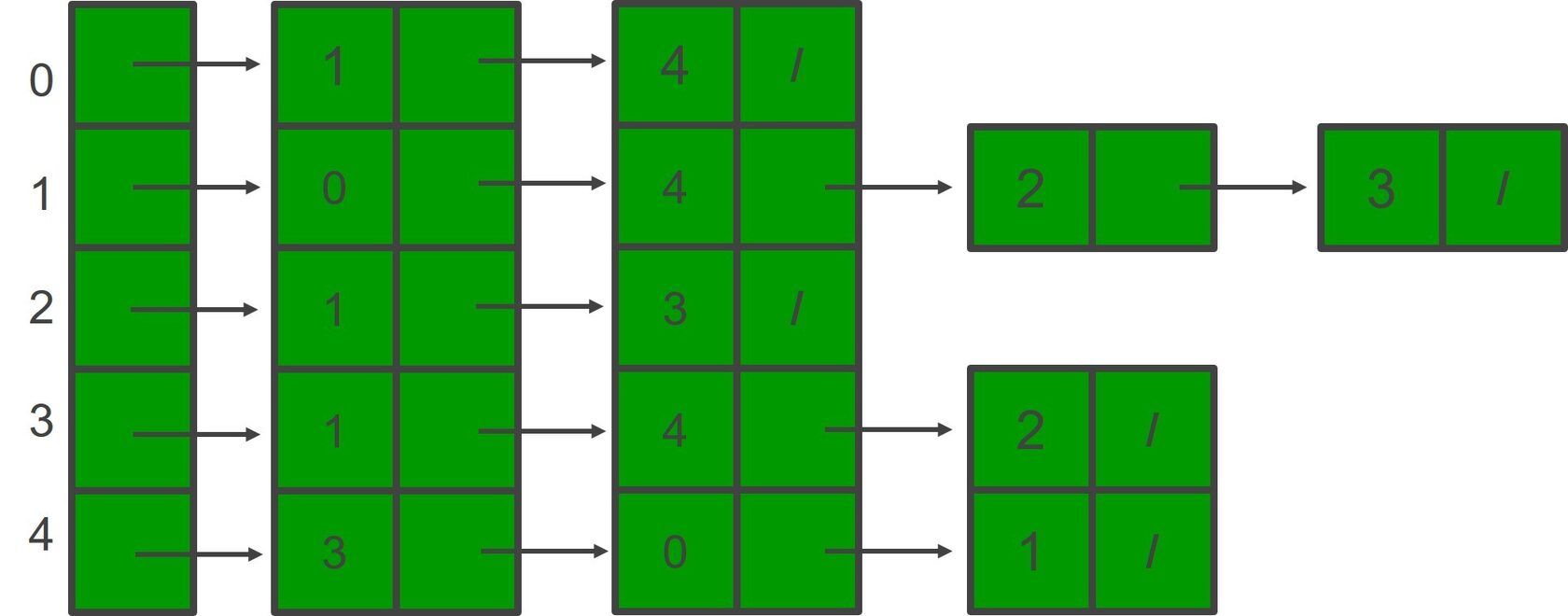
Тут идеально подходит словарь, где:
Для взвешенных графов значением может быть список кортежей `(сосед, вес_ребра)`.
- Ключ: Вершина (может быть числом, строкой, любым хешируемым объектом).
- Значение: Список (или множество) вершин-соседей.
Для взвешенных графов значением может быть список кортежей `(сосед, вес_ребра)`.
Использование `collections.defaultdict(list)` (или `defaultdict(set)`) упрощает код, так как не нужно проверять наличие вершины в словаре перед добавлением первого соседа.
Пример:
from collections import defaultdict
# Используем defaultdict(list)
adj_list = defaultdict(list)
edges = [(0, 1), (0, 4), (1, 2), (1, 3), (1, 4), (2, 3), (3, 4)]
# Заполняем список смежности
for u, v in edges:
adj_list[u].append(v)
adj_list[v].append(u) # Для неориентированного графа
print("Список смежности:")
# Выводим содержимое словаря
for vertex in sorted(adj_list.keys()): # Сортируем ключи для предсказуемого вывода
print(f"Вершина {vertex}: {sorted(adj_list[vertex])}") # Сортируем соседей для наглядности
# Пример вывода:
# Вершина 0: [1, 4]
# Вершина 1: [0, 2, 3, 4]
# Вершина 2: [1, 3]
# Вершина 3: [1, 2, 4]
# Вершина 4: [0, 1, 3]
# Получение соседей вершины 1: O(1) в среднем для словаря
print(f"\nСоседи вершины 1: {adj_list[1]}")
# Проверка ребра (1, 4): O(k), где k - степень вершины 1
print(f"Ребро (1, 4) существует? {'Да' if 4 in adj_list[1] else 'Нет'}")Итак, у нас есть два основных способа представления графа. Какой же выбрать?
Какой способ выбрать? Матрица или список?
Выбор между матрицей смежности и списком смежности зависит от характеристик графа и операций, которые вы планируете выполнять чаще всего:
Матрица смежности
- Лучше для: плотных графов (много рёбер, E близко к V²).
- Лучше, если: Критически важна мгновенная проверка (O(1)) наличия ребра между любыми двумя вершинами.
- Хуже для: Разреженных графов (тратит много памяти зря), динамических графов (где часто добавляются/удаляются вершины).
Список смежности
- Лучше для: разреженных графов (подавляющее большинство реальных графов — разреженные) или динамических графов, так как добавление/удаление вершин и рёбер проще и быстрее.
- Лучше, если: Важен быстрый доступ ко всем соседям вершины (O(1) до списка + O(k) для итерации).
- Популярность: В Python список смежности (обычно на `defaultdict`) является стандартным и наиболее идиоматичным способом представления графов из-за его эффективности по памяти и гибкости для типичных разреженных графов.
Вывод
В большинстве случаев для Python выбирайте список смежности. Матрицу смежности стоит рассматривать только при специфических требованиях к плотным графам или O(1) проверке рёбер.
Теперь, когда мы умеем представлять графы в коде (и выбрали список смежности как основной способ), самое время научиться их систематически обходить, чтобы посетить все достижимые вершины. Переходим к алгоритмам обхода!
Обходим графы: BFS и DFS
Представив граф в виде списка смежности, мы можем начать его исследовать. Обход графа — это процесс систематического посещения всех достижимых из стартовой точки вершин. Как и в деревьях, два основных метода — BFS и DFS.
Ключевое отличие от деревьев: графы могут содержать циклы! Если мы не будем осторожны, мы можем бесконечно ходить по кругу A -> B -> C -> A.... Поэтому для любого алгоритма обхода графа абсолютно необходимо отслеживать уже посещённые вершины, чтобы не обрабатывать их повторно и не зацикливаться. Обычно для этого используют множества.
Обход в ширину (BFS)
Идея BFS для графов та же, что и для деревьев: исследуем граф "по слоям", двигаясь от стартовой вершины `s`. Сначала посещаем `s`, затем всех её соседей (слой 1), затем всех непосещённых соседей узлов слоя 1 (слой 2), и так далее. Используем очередь (deque) и множество visited.
Алгоритм BFS:
- Выбрать стартовую вершину `s`.
- Создать пустую очередь `queue` (`deque([s])`) и добавить в неё `s`.
- Создать пустое множество `visited` и добавить в него `s`.
- Пока `queue` не пуста:
- Извлечь вершину `u` из начала `queue` (`popleft()`).
- Обработать `u` (например, добавить в результат).
- Для каждого соседа `v` вершины `u`:
- Если `v` не в `visited`:
- Добавить `v` в `visited`.
- Добавить `v` в конец `queue` (`append()`).
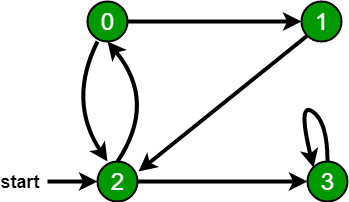
Реализация BFS:
from collections import defaultdict, deque
class Graph:
def __init__(self):
self.graph = defaultdict(list) # Список смежности
def add_edge(self, u, v, is_directed=False):
"""Добавляет ребро между u и v."""
self.graph[u].append(v)
if not is_directed:
self.graph[v].append(u) # Для неориентированного
def bfs(self, start_node):
"""Выполняет BFS графа, начиная с start_node."""
if start_node not in self.graph:
print(f"Стартовая вершина {start_node} отсутствует.")
return []
visited = {start_node} # Используем set для O(1) проверки
queue = deque([start_node])
result_order = [] # Список для хранения порядка обхода
while queue:
current_node = queue.popleft()
result_order.append(current_node) # Обрабатываем
for neighbor in self.graph[current_node]:
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)
print(f"BFS от {start_node}: {result_order}")
return result_order
# --- Создаем граф (ориентированный) ---
# 0 -> 1, 0 -> 2
# 1 -> 2
# 2 -> 0, 2 -> 3
# 3 -> 3
g_bfs = Graph()
g_bfs.add_edge(0, 1, is_directed=True)
g_bfs.add_edge(0, 2, is_directed=True)
g_bfs.add_edge(1, 2, is_directed=True)
g_bfs.add_edge(2, 0, is_directed=True) # Цикл!
g_bfs.add_edge(2, 3, is_directed=True)
g_bfs.add_edge(3, 3, is_directed=True) # Петля!
-
g_bfs.bfs(2)
# Ожидаемый вывод: BFS от 2: [2, 0, 3, 1]Для чего используется BFS?
- Находит кратчайший путь (по числу рёбер) в невзвешенном графе от стартовой вершины до всех остальных.
- Используется для проверки связности графа.
- Применяется в алгоритмах поиска пути (например, алгоритм Ли для поиска в сетке).
Обход в глубину (DFS)
Обход в глубину (Depth-First Search, DFS) для графов работает по тому же принципу, что и для деревьев: выбираем путь и идем по нему максимально глубоко, пока не упремся в тупик (вершину без непосещенных соседей) или не вернемся в уже посещенную вершину. Затем "отступаем" назад и пробуем другие пути.
И снова, из-за возможных циклов, критически важно использовать множество для отслеживания посещённых вершин.
Придерживаемся такого алгоритма:
Функция `dfs_recursive(vertex, visited)` будет работать так:
- Создать пустое множество `visited`.
- Выбрать стартовую вершину `s`.
- Вызвать вспомогательную рекурсивную функцию `dfs_recursive(vertex, visited)`.
Функция `dfs_recursive(vertex, visited)` будет работать так:
- Пометить vertex как посещённую (visited.add(vertex)).
- Обработать vertex (например, добавить в результат).
- Для каждого соседа neighbor вершины vertex:
- Если neighbor не в visited:
- Рекурсивно вызвать dfs_recursive(neighbor, visited).
Рекурсивная реализация DFS:
from collections import defaultdict
class Graph: # Используем тот же класс, что и для BFS
def __init__(self):
self.graph = defaultdict(list)
self.dfs_result_order = [] # Для хранения результата обхода
def add_edge(self, u, v, is_directed=False):
self.graph[u].append(v)
if not is_directed:
self.graph[v].append(u)
# Вспомогательная рекурсивная функция
def _dfs_recursive(self, vertex, visited):
visited.add(vertex) # 1. Пометить
self.dfs_result_order.append(vertex) # 2. Обработать
# 3. Для каждого соседа
for neighbor in self.graph[vertex]:
# 4. Если не посещен
if neighbor not in visited:
# 5. Рекурсивный вызов
self._dfs_recursive(neighbor, visited)
def dfs(self, start_node):
"""Выполняет DFS графа, начиная с start_node."""
if start_node not in self.graph:
print(f"Стартовая вершина {start_node} отсутствует.")
return []
visited = set()
self.dfs_result_order = [] # Очищаем результат перед новым обходом
self._dfs_recursive(start_node, visited) # Запускаем рекурсию
print(f"DFS от {start_node}: {self.dfs_result_order}")
return self.dfs_result_order
g_dfs = Graph()
g_dfs.add_edge(0, 1, is_directed=True); g_dfs.add_edge(0, 2, is_directed=True)
g_dfs.add_edge(1, 2, is_directed=True)
g_dfs.add_edge(2, 0, is_directed=True) # Цикл 0-2-0
g_dfs.add_edge(2, 3, is_directed=True)
g_dfs.add_edge(3, 3, is_directed=True) # Петля
g_dfs.dfs(2)
# DFS от 2: [2, 0, 1, 3]
# (Порядок может отличаться от BFS, т.к. DFS уходит вглубь: 2 -> 0 -> 1, затем возвращается и идет 2 -> 3)Для чего используется DFS?
Возможна и итеративная реализация с использованием явного стека (`list` или `deque`) вместо стека вызовов, что может быть полезно для избежания `RecursionError` на очень глубоких графах.
- Поиск пути между двумя вершинами.
- Обнаружение циклов в графе.
- Топологическая сортировка для DAG (ориентированных ациклических графов) — упорядочивание задач с зависимостями.
- Поиск сильно связных компонент в ориентированных графах.
Возможна и итеративная реализация с использованием явного стека (`list` или `deque`) вместо стека вызовов, что может быть полезно для избежания `RecursionError` на очень глубоких графах.
BFS vs. DFS: краткое Сравнение
Хотя и BFS, и DFS посещают все достижимые вершины и имеют одинаковую асимптотическую временную сложность O(V+E), их поведение и области применения различаются:
- Структура данных: BFS использует очередь, DFS использует стек(неявно через рекурсию или явно при итеративной реализации).
- Порядок обхода: BFS исследует граф по уровням, равномерно удаляясь от старта. DFS уходит вглубь по одному пути до упора, прежде чем исследовать другие ветви.
- Кратчайший путь: BFS находит кратчайший путь в невзвешенном графе. DFS не гарантирует нахождение кратчайшего пути.
- Память: BFS может требовать больше памяти для "широких" графов (много узлов на одном уровне). DFS может требовать больше памяти (стека) для "длинных" путей или глубоких графов.
Выбор между BFS и DFS зависит от конкретной задачи и структуры графа.
Заключение: графы освоены🏆
Вот и она — финишная черта нашего основного марафона! Мы прошли долгий путь: от неизменяемых строк и байтов до гибких списков и deque. Разобрались с хеш-таблицами в dict и set. Покорили рекурсию и освоили её оптимизацию через динамическое программирование. Научились эффективно искать и сортировать данные. Построили и обошли деревья, BST и кучи. И наконец, связали всё воедино с помощью графов.
Понимание внутреннего устройства, асимптотической сложности (Big O) и алгоритмов работы с ними — это не академическая прихоть, а фундамент для написания по-настоящему эффективного, масштабируемого и элегантного кода на Python.
Знание алгоритмов и структур данных позволяет вам не просто решать задачи, а решать их правильно.
Надеюсь, этот цикл статей был для вас полезным и интересным 🎉
