После поиска и сортировки в линейных коллекциях (Часть 4), пора перейти к нелинейным структурам. Файловые системы, DOM, оргструктуры — всё это иерархии, для моделирования которых в программировании служат деревья (trees). Понимание деревьев — ключ к эффективной работе с иерархическими данными и многим продвинутым алгоритмам.
Сегодня мы разберем основы деревьев, сфокусируемся на бинарных деревьях, научимся их обходить (DFS/BFS), изучим бинарные деревья поиска (BST), коснёмся куч (heaps) и модуля `heapq`.
Весь маршрут нашего гайда:
🌳 Начнем с базовой терминологии.
Введение в деревья
Мы ранее рассматривали линейные структуры — списки, очереди, стеки, где элементы выстроены "в ряд", один за другим. А как быть с нелинейными, иерархическими отношениями, как, например, структура папок на диске или DOM веб-страницы? Для моделирования таких отношений в программировании используется структура данных под названием дерево. В отличие от списка, где у каждого элемента (кроме первого и последнего) есть ровно один предыдущий и один следующий, в дереве у одного "родительского" элемента может быть несколько "дочерних" элементов, образуя ветвящуюся структуру.
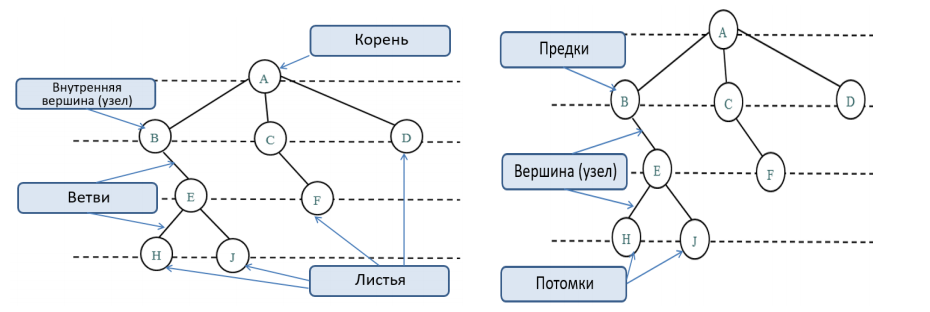
Представьте перевернутое настоящее дерево: у него есть один главный корень (вершина иерархии), от которого отходят ветви (связи), ведущие к другим узлам (элементам данных), которые, в свою очередь, могут иметь свои ветви и узлы, пока мы не дойдем до листьев (узлов без потомков).
Представьте перевернутое настоящее дерево: у него есть один главный корень (вершина иерархии), от которого отходят ветви (связи), ведущие к другим узлам (элементам данных), которые, в свою очередь, могут иметь свои ветви и узлы, пока мы не дойдем до листьев (узлов без потомков).
Чтобы говорить о деревьях на одном языке, нам нужно знать несколько ключевых терминов:
- Узел (Node): Основной строительный блок дерева. Каждый узел содержит какие-то данные (значение, ключ) и ссылки на другие узлы (своих потомков).
- Корень (Root): Самый верхний узел дерева, у которого нет родителя. С него начинается обход или работа с деревом. У дерева всегда только один корень.
- Ребро (Edge): Связь между двумя узлами. Обычно представляет собой ссылку от родительского узла к дочернему.
- Родитель (Parent): Узел, имеющий хотя бы одного потомка. У любого узла (кроме корня) есть ровно один родитель.
- Потомок (Child): Узел, на который есть прямая ссылка от другого узла (родителя) при движении от корня.
- Сиблинги (Siblings) / Братья-Сестры: Узлы, имеющие одного и того же родителя.
- Лист (Leaf): Узел, у которого нет потомков. Это конечные узлы дерева.
- Поддерево (Subtree): Часть дерева, состоящая из некоторого узла и всех его потомков (включая их связи). Этот узел является корнем поддерева.
- Путь (Path): Последовательность узлов и ребер от одного узла к другому.
- Глубина (Depth) узла: Длина пути (количество ребер) от корня дерева до этого узла. Глубина корня равна 0.
- Высота (Height) узла: Длина самого длинного пути от этого узла до листа в его поддереве. Высота листа равна 0.
- Высота Дерева: Высота корневого узла. Это максимальная глубина любого узла в дереве.
Понимание этих терминов критически важно для обсуждения и реализации алгоритмов на деревьях. Теперь давайте перейдем к самому распространенному типу деревьев — бинарным деревьям.
Бинарные деревья: не более двух потомков ✌️
Среди разных видов деревьев особое место занимают бинарные Деревья (binary trees). Их ключевая особенность: у каждого узла не более ДВУХ потомков, традиционно называемых левым (left) и правым (right). Любой из потомков (или оба сразу) может отсутствовать (в реализации это обычно означает, что соответствующая ссылка равна `None`).
Почему бинарные деревья важны?
- Простота структуры: Ограничение на два потомка упрощает структуру узла и алгоритмы работы с деревом.
- Основа для эффективных структур: Многие важные и эффективные структуры данных являются бинарными деревьями или основаны на них. Самые известные примеры:
- Бинарные деревья поиска (BST): Используют упорядоченность для быстрого поиска O(log n).
- Бинарные кучи (binary heaps): Основа для очередей с приоритетом (модуль `heapq` как раз реализует бинарную кучу).
- Деревья выражений: Используются для представления и вычисления математических или логических выражений.
- Частое применение: Они возникают во многих алгоритмах, от сжатия данных (деревья Хаффмана) до 3D-графики (BSP-деревья).
Из-за их распространенности и важности, мы сосредоточим большую часть нашего внимания именно на бинарных деревьях. И первый шаг — понять, как представить узел такого дерева в коде.
Реализация узла
Узел бинарного дерева должен хранить данные и ссылки на левого и правого потомков. Создадим для этого простой класс `TreeNode`.
class TreeNode:
"""Представляет узел бинарного дерева."""
def __init__(self, key):
self.key = key # Данные узла
self.left = None # Ссылка на левого потомка
self.right = None # Ссылка на правого потомка
def __repr__(self):
"""Строковое представление узла (показывает ключ)."""
return f"Node({self.key})"Пояснения:
Этот простой класс `TreeNode` — наш основной "кирпичик" для построения любых бинарных деревьев, включая деревья выражений, BST и другие. Теперь посмотрим, как из этих кирпичиков можно собрать целое дерево.
- `__init__(self, key)`: Конструктор принимает `key` — это значение, которое будет храниться в узле. Мы сохраняем его в атрибуте `self.key`.
- `self.left = None и self.right = None`: При создании узла мы не знаем, какие у него будут потомки, поэтому инициализируем ссылки на них значением `None`. Позже мы сможем присвоить этим атрибутам другие объекты `TreeNode`.
- `__repr__(self)`: Этот "магический" метод определяет, как объект будет представлен в виде строки, например, при выводе в консоли или при печати списка узлов. `f"Node({self.key})"` даст нам понятное представление вроде `Node(50)` или `Node('+')`.
Этот простой класс `TreeNode` — наш основной "кирпичик" для построения любых бинарных деревьев, включая деревья выражений, BST и другие. Теперь посмотрим, как из этих кирпичиков можно собрать целое дерево.
Создание дерева вручную
Хотя в реальных задачах деревья часто строятся динамически (например, при вставке элементов в BST или при парсинге данных), создание небольшого дерева вручную — отличный способ понять, как узлы связываются друг с другом через атрибуты `left` и `right`.
Давайте построим дерево, представляющее арифметическое выражение `(1 + 2) * 3`. В таком дереве внутренние узлы будут операторами (`*`, `+`), а листья — операндами (числами 1, 2, 3).
Структура дерева:
* <-- Корень
/ \
+ 3 <-- Узел '+' и лист '3'
/ \
1 2 <-- Листья '1' и '2'Код для построения:
# 1. Узлы-листья (операнды)
node1, node2, node3 = TreeNode(1), TreeNode(2), TreeNode(3)
# 2. Узлы-операторы
node_plus, node_multiply = TreeNode('+'), TreeNode('*')
# 3. Строим связи
node_plus.left, node_plus.right = node1, node2
node_multiply.left, node_multiply.right = node_plus, node3
# 4. Корень дерева
root_expression_tree = node_multiply
print(f"Корень дерева: {root_expression_tree}")
# Пример доступа: root_expression_tree.left -> Node(+), root_expression_tree.left.left -> Node(1)Мы присвоили созданные узлы атрибутам `left` и `right` их будущих родителей. Корень дерева (`root_expression_tree`) — это просто ссылка на самый верхний узел (`node_multiply`), через которую мы можем получить доступ ко всей структуре.
Теперь, когда у нас есть дерево, возникает вопрос: как систематически посетить все его узлы, например, чтобы вычислить значение выражения или просто вывести все элементы? Для этого нам нужны алгоритмы обхода деревьев. Переходим к ним!
Теперь, когда у нас есть дерево, возникает вопрос: как систематически посетить все его узлы, например, чтобы вычислить значение выражения или просто вывести все элементы? Для этого нам нужны алгоритмы обхода деревьев. Переходим к ним!
Как обойти дерево?
Просто создать дерево недостаточно. Нам нужны способы посетить каждый узел ровно один раз для выполнения какой-либо операции (печать, вычисление, поиск и т.д.). Беспорядочное перемещение по ссылкам `left` и `right` не гарантирует полного и однократного посещения. Для этого существуют алгоритмы обхода (traversal algorithms).
Два основных подхода — обход в Глубину (DFS), идущий по ветвям до конца, и обход в ширину (BFS), идущий по уровням. Оба гарантируют посещение каждого узла ровно раз, но в разном порядке.
Обход в глубину (DFS)
Обход в глубину (Depth-First Search, DFS) исследует ветви дерева настолько глубоко, насколько это возможно, прежде чем вернуться и исследовать другие ветви. Это очень естественный подход для рекурсивной реализации.
Для бинарных деревьев существует три основных варианта DFS, которые различаются порядком посещения (обработки) текущего узла относительно рекурсивного обхода его левого и правого поддеревьев:
- In-order (LNR): Сначала левое поддерево, потом узел, потом правое (идеально для получения отсортированной последовательности из BST).
- Pre-order (NLR): Сначала узел, потом левое, потом правое поддерево (полезно для копирования дерева, префиксной записи).
- Post-order (LRN): Сначала левое, потом правое поддерево, потом узел (подходит для удаления узлов, постфиксной записи).
Рекурсия здесь — самый элегантный и понятный способ реализации, так как она точно отражает определения обходов.
def inorder(node):
"""In-order (LNR) обход."""
return inorder(node.left) + [node.key] + inorder(node.right) if node else []
def preorder(node):
"""Pre-order (NLR) обход."""
return [node.key] + preorder(node.left) + preorder(node.right) if node else []
def postorder(node):
"""Post-order (LRN) обход."""
return postorder(node.left) + postorder(node.right) + [node.key] if node else []
# --- Тестовое дерево ---
# F
# / \
# B G
# / \ \
# A D I
# / \ /
# C E H
root = TreeNode('F')
root.left = TreeNode('B'); root.right = TreeNode('G')
root.left.left = TreeNode('A'); root.left.right = TreeNode('D')
root.left.right.left = TreeNode('C'); root.left.right.right = TreeNode('E')
root.right.right = TreeNode('I'); root.right.right.left = TreeNode('H')
print(f"In-order (LNR): {inorder(root)}")
# ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
print(f"Pre-order (NLR): {preorder(root)}")
# ['F', 'B', 'A', 'D', 'C', 'E', 'G', 'I', 'H']
print(f"Post-order (LRN): {postorder(root)}")
# ['A', 'C', 'E', 'D', 'B', 'H', 'I', 'G', 'F']Как видите, порядок посещения узлов для каждого типа обхода уникален. Рекурсивная реализация очень компактна и следует прямо из определения.
Обход в ширину (BFS)
Обход в ширину (Breadth-First Search, BFS), также известный как обход по уровням (Level-Order Traversal), исследует дерево совершенно иначе, чем DFS. Вместо того чтобы углубляться в одну ветку, BFS посещает узлы горизонтально, уровень за уровнем:
- Сначала посещается корень (уровень 0).
- Затем посещаются все прямые потомки корня (уровень 1), слева направо.
- Затем все узлы на уровне 2 (потомки узлов уровня 1), слева направо.
- И так далее, пока не будут посещены все узлы на всех уровнях.
Как реализовать BFS? С помощью очереди! Рекурсия здесь не так удобна, как для DFS. Идеальным инструментом для реализации BFS является очередь, работающая по принципу FIFO (First-In, First-Out). Мы будем использовать `collections.deque` для эффективности.
Алгоритм BFS:
- Если дерево пустое (корень `None`), завершить работу.
- Создать пустую очередь (`deque`).
- Добавить корень дерева в очередь.
- Пока очередь не пуста:
- Извлечь узел (`current_node`) из начала очереди (`popleft()`).
- Обработать `current_node` (например, добавить его ключ в результат).
- Если у `current_node` есть левый потомок, добавить его в конец очереди (`append()`).
- Если у `current_node` есть правый потомок, добавить его в конец очереди (`append()`).
Этот процесс гарантирует, что мы сначала обработаем все узлы текущего уровня, прежде чем перейти к узлам следующего уровня, так как потомки добавляются в конец очереди и будут извлечены только после того, как все узлы их уровня будут обработаны.
Реализация BFS (итеративно с deque):
from collections import deque
def level_order(root):
"""BFS (Level-Order) обход."""
if not root: return []
result = []
nodes_queue = deque([root])
while nodes_queue:
current_node = nodes_queue.popleft()
result.append(current_node.key)
if current_node.left:
nodes_queue.append(current_node.left)
if current_node.right:
nodes_queue.append(current_node.right)
return result
print(f"Level-order (BFS): {level_order(root)}")
# Ожидаемый вывод: ['F', 'B', 'G', 'A', 'D', 'I', 'C', 'E', 'H']Заметьте, узлы посещаются строго по уровням: F (уровень 0), B G (уровень 1), A D I (уровень 2), C E H (уровень 3).
BFS часто используется для поиска кратчайшего пути в не взвешенных графах (или деревьях), так как он исследует все пути одинаковой длины одновременно.
Теперь, когда мы знаем разные способы обхода, давайте кратко сравним их сложность и применение.
BFS часто используется для поиска кратчайшего пути в не взвешенных графах (или деревьях), так как он исследует все пути одинаковой длины одновременно.
Теперь, когда мы знаем разные способы обхода, давайте кратко сравним их сложность и применение.
Сложность и выбор обхода
Все четыре рассмотренных алгоритма обхода — In-order (DFS), Pre-order (DFS), Post-order (DFS) и Level-order (BFS) — выполняют основную задачу: посещают каждый узел дерева ровно один раз.
Поскольку каждый узел и каждое ребро (связь между узлами) обрабатываются примерно константное количество раз (например, посещение узла, переход по ссылке), временная сложность всех четырех обходов одинакова и составляет O(n), где n — количество узлов в дереве. Это оптимально, так как нам в любом случае нужно посмотреть на каждый узел.
А вот по требованиям к памяти они различаются:
- Рекурсивные DFS (In, Pre, Post): Используют стек вызовов для хранения информации о рекурсивных вызовах. Глубина этого стека равна высоте дерева (`h`). В лучшем случае (для идеально сбалансированного бинарного дерева) высота `h` примерно равна log n, и пространственная сложность составляет O(log n). В худшем случае (для вырожденного дерева, похожего на связанный список) высота h может достигать n, и пространственная сложность становится O(n).
- Итеративный BFS (Level-Order): Использует очередь (deque) для хранения узлов, которые предстоит посетить. В худшем случае (для "широкого", полного или почти полного дерева) на последнем уровне может находиться примерно n/2 узлов, и все они одновременно окажутся в очереди. Поэтому пространственная сложность BFS в худшем случае составляет O(w), где w - максимальная ширина дерева, что может достигать O(n).
Когда какой обход выбрать?
Выбор алгоритма обхода зависит от задачи, которую вы решаете:
Выбор алгоритма обхода зависит от задачи, которую вы решаете:
- In-order (Лево-Корень-Право): Используйте его в первую очередь для бинарных деревьев поиска, так как он позволяет получить элементы в отсортированном порядке.
- Pre-order (Корень-Лево-Право): Применяйте для задач копирования дерева, получения префиксной записи математических выражений (где оператор идет перед операндами) или в алгоритмах, где важно сначала обработать родительский узел перед его потомками.
- Post-order (Лево-Право-Корень): Часто используется для безопасного удаления узлов дерева (когда сначала нужно обработать/удалить потомков) или для получения постфиксной (обратной польской) записи выражений (где оператор идет после операндов).
- BFS / Level-order: Выбирайте для задач, где важны уровни дерева, для поиска кратчайшего пути от корня (в терминах количества ребер) в не взвешенных деревьях/графах, а также в некоторых других алгоритмах на графах.
Знание этих обходов и их свойств — ключ к эффективной работе с древовидными структурами.
Бинарные деревья поиска (BST)
Обычные бинарные деревья позволяют хранить иерархические данные, но они не очень помогают, если нам нужно быстро найти конкретный элемент. Придется использовать один из обходов (DFS или BFS), что займет в среднем O(n) времени.
Бинарное дерево поиска решает эту проблему, добавляя к структуре бинарного дерева важное свойство упорядоченности. Для любого узла N в BST:
- Все ключи (значения) в левом поддереве узла N строго меньше (<) ключа узла N.
- Все ключи (значения) в правом поддереве узла N строго больше (>) ключа узла N.
- Левое и правое поддеревья узла N также являются бинарными деревьями поиска (свойство выполняется рекурсивно).
Важное замечание о дубликатах
Классическое определение BST часто не допускает дубликатов ключей. Если дубликаты нужны, их обработку нужно четко определить: либо игнорировать, либо хранить счетчик, либо последовательно помещать их только в одно из поддеревьев (например, в правое, используя >=). Для простоты мы будем придерживаться варианта без дубликатов.
Пример BST:
50 <-- Корень
/ \
30 70 <-- (30 < 50), (70 > 50)
/ \ / \
20 40 60 80 <-- (20<30), (40>30); (60<70), (80>70)Обратите внимание: для любого узла это правило выполняется. Например, для корня 50 все узлы слева (30, 20, 40) меньше 50, а все узлы справа (70, 60, 80) больше 50. Для узла 30: слева 20 (< 30), справа 40 (> 30).
Именно свойство упорядоченности позволяет BST выполнять операции поиска, вставки и (с некоторыми оговорками) удаления очень быстро — в среднем за O(log n) времени, где n — количество узлов в дереве. Это сравнимо со скоростью бинарного поиска в отсортированном массиве!
Давайте посмотрим, как работает поиск в BST.
Именно свойство упорядоченности позволяет BST выполнять операции поиска, вставки и (с некоторыми оговорками) удаления очень быстро — в среднем за O(log n) времени, где n — количество узлов в дереве. Это сравнимо со скоростью бинарного поиска в отсортированном массиве!
Давайте посмотрим, как работает поиск в BST.
Поиск в BST
Алгоритм поиска ключа (`target`) в бинарном дереве поиска элегантен и очень похож на бинарный поиск в массиве:
Шаги 5 и 6 взаимоисключающие, и подразумевают либо рекурсивный вызов, либо продолжение итеративного цикла, что приводит к шагу 2 на следующем уровне.
- Начать с корня: Установить `current_node` равным корню дерева.
- Проверка: Если `current_node` равен `None`, значит, элемент не найден (или дерево пусто). Вернуть `None` или `False`.
- Сравнение: Сравнить `target` с `current_node.key`.
- Принятие решения: Если `target == current_node.key`, то элемент найден. Вернуть `current_node` или `True`.
- Выбор пути (если не найден): Если `target < current_node.key`, то элемент может быть только в левом поддереве. Рекурсивно вызвать поиск для `current_node.left` (или в итеративной версии присвоить `current_node = current_node.left` и вернуться к шагу 2).
- Выбор пути (продолжение): Если `target > current_node.key`, то элемент может быть только в правом поддереве. Рекурсивно вызвать поиск для `current_node.right` (или в итеративной версии присвоить `current_node = current_node.right` и вернуться к шагу 2).
Шаги 5 и 6 взаимоисключающие, и подразумевают либо рекурсивный вызов, либо продолжение итеративного цикла, что приводит к шагу 2 на следующем уровне.
Рекурсия здесь очень наглядно отражает логику "идти влево или вправо":
def search_bst(node, target):
"""Ищет target в BST (рекурсивно). Возвращает узел или None."""
if node is None or node.key == target: # Базовые случаи: не нашли или нашли
return node
elif target < node.key:
return search_bst(node.left, target) # Идем влево
else: # target > node.key
return search_bst(node.right, target) # Идем вправо
# --- Создаем BST ---
# 50
# / \
# 30 70 ... и т.д. (как в пред. примере)
root_bst = TreeNode(50)
root_bst.left = TreeNode(30); root_bst.right = TreeNode(70)
root_bst.left.left = TreeNode(20); root_bst.left.right = TreeNode(40)
root_bst.right.left = TreeNode(60); root_bst.right.right = TreeNode(80)
key_to_find = 40
found_node = search_bst(root_bst, key_to_find)
print(f"Поиск {key_to_find}: {'Найден' if found_node else 'Не найден'}")
key_to_find = 99
found_node = search_bst(root_bst, key_to_find)
print(f"Поиск {key_to_find}: {'Найден' if found_node else 'Не найден'}")На каждом шаге сравнения мы отбрасываем целое поддерево — либо левое, либо правое. Если дерево сбалансировано (то есть его высота примерно равна log n, где n — количество узлов), то количество шагов, необходимых для нахождения элемента или установления его отсутствия, будет пропорционально высоте дерева, то есть O(log n). Это такой же порядок эффективности, как у бинарного поиска в отсортированном массиве.
Но есть нюанс... Скорость O(log n) достигается только для сбалансированных деревьев. А что если дерево не сбалансировано?
Но есть нюанс... Скорость O(log n) достигается только для сбалансированных деревьев. А что если дерево не сбалансировано?
Проблема баланса
Скорость O(log n) для операций в BST достигается только тогда, когда дерево сбалансировано. Сбалансированное дерево — это такое дерево, у которого высота левого и правого поддеревьев для любого узла различается не более чем на некоторую константу (в идеале, они почти равны). В этом случае высота всего дерева h действительно близка к log n.
Что если вставлять элементы в уже отсортированном порядке (например, 10, 20, 30, 40...)? Каждый новый элемент будет уходить вправо, и дерево выродится в структуру, похожую на связанный список:
10
\
20
\
30
\
40
\
50В таком дереве нет никакого ветвления. Чтобы найти элемент 50, нам придется пройти по всем узлам от корня 10 до самого конца. Поиск (а также вставка и удаление) в таком вырожденном BST превращается в линейный поиск со сложностью O(n) в худшем случае! Вся магия логарифмической скорости теряется. То же самое произойдет, если вставлять элементы в обратно отсортированном порядке (дерево "вытянется" влево).
Чтобы гарантировать логарифмическую сложность O(log n) для всех операций даже в худшем случае, были разработаны самобалансирующиеся бинарные деревья поиска.
Это такие BST, которые при выполнении операций вставки и удаления автоматически выполняют специальные операции балансировки (обычно "повороты" — `tree rotations`), чтобы поддерживать дерево в сбалансированном состоянии (то есть гарантировать, что его высота не превышает C * log n, где C — некоторая константа).
Наиболее известные типы самобалансирующихся BST:
Нужно ли реализовывать их самому?
Реализация самобалансирующихся деревьев — задача нетривиальная и подверженная ошибкам. В стандартной библиотеке Python нет встроенной реализации AVL или красно-чёрных деревьев (в отличие от C++ или Java). Для большинства повседневных задач достаточно встроенных `dict` и `set` (которые используют хеш-таблицы) или работы с отсортированными списками через `bisect`.
Однако, если вам действительно нужна структура данных с гарантированной логарифмической сложностью для всех операций поиска, вставки, удаления и получения упорядоченной последовательности, вам придется либо найти стороннюю библиотеку (например, `sortedcontainers`), либо реализовать самобалансирующееся дерево самостоятельно (что выходит за рамки этого базового гайда).
Итого: BST обеспечивают O(log n) в среднем, но O(n) в худшем случае (при дисбалансе). Самобалансирующиеся деревья гарантируют O(log n) всегда, но сложнее в реализации.
Теперь, когда мы понимаем поиск и проблему баланса, давайте посмотрим, как добавлять новые элементы в (обычное) BST.
Чтобы гарантировать логарифмическую сложность O(log n) для всех операций даже в худшем случае, были разработаны самобалансирующиеся бинарные деревья поиска.
Это такие BST, которые при выполнении операций вставки и удаления автоматически выполняют специальные операции балансировки (обычно "повороты" — `tree rotations`), чтобы поддерживать дерево в сбалансированном состоянии (то есть гарантировать, что его высота не превышает C * log n, где C — некоторая константа).
Наиболее известные типы самобалансирующихся BST:
- AVL-деревья (Adelson-Velsky and Landis' trees): Самые первые самобалансирующиеся деревья. Очень строго поддерживают баланс (высоты левого и правого поддеревьев любого узла могут отличаться не более чем на 1). Это гарантирует минимальную высоту, но операции вставки/удаления могут требовать больше поворотов.
- Красно-чёрные деревья (Red-Black Trees): Используют более "мягкие" правила балансировки (основанные на "цвете" узлов — красный или черный). Они могут быть чуть менее сбалансированными, чем AVL-деревья (высота может быть до 2 * log n), но операции вставки/удаления обычно требуют меньше поворотов и выполняются быстрее на практике. Именно красно-чёрные деревья часто используются в реализациях стандартных библиотек разных языков.
Нужно ли реализовывать их самому?
Реализация самобалансирующихся деревьев — задача нетривиальная и подверженная ошибкам. В стандартной библиотеке Python нет встроенной реализации AVL или красно-чёрных деревьев (в отличие от C++ или Java). Для большинства повседневных задач достаточно встроенных `dict` и `set` (которые используют хеш-таблицы) или работы с отсортированными списками через `bisect`.
Однако, если вам действительно нужна структура данных с гарантированной логарифмической сложностью для всех операций поиска, вставки, удаления и получения упорядоченной последовательности, вам придется либо найти стороннюю библиотеку (например, `sortedcontainers`), либо реализовать самобалансирующееся дерево самостоятельно (что выходит за рамки этого базового гайда).
Итого: BST обеспечивают O(log n) в среднем, но O(n) в худшем случае (при дисбалансе). Самобалансирующиеся деревья гарантируют O(log n) всегда, но сложнее в реализации.
Теперь, когда мы понимаем поиск и проблему баланса, давайте посмотрим, как добавлять новые элементы в (обычное) BST.
Вставка в BST
Идея вставки нового ключа (`key_to_insert`) в BST очень похожа на алгоритм поиска. Нам нужно найти первое "пустое" место (где ссылка `left` или `right` равна `None`), куда можно было бы прикрепить новый узел, следуя правилу "меньше налево, больше направо". Алгоритм такой:
- Если дерево пустое, новый узел становится корнем.
- Начать с корня.
- Сравнить `key_to_insert` с ключом текущего узла.
- Если ключ равен – (в нашей реализации без дубликатов) ничего не делать и завершить.
- Если `key_to_insert` меньше – перейти к левому потомку. Если левого потомка нет, вставить новый узел сюда.
- Если `key_to_insert` больше – перейти к правому потомку. Если правого потомка нет, вставить новый узел сюда.
- Повторять шаги 3-6, пока узел не будет вставлен.
Рекурсивный подход здесь снова выглядит компактно. Функция будет возвращать узел, который должен занять место текущего узла в дереве (это может быть сам текущий узел, если поддерево под ним изменилось, или новый узел, если мы вставляем в пустое место).
def insert_bst(node, key_to_insert):
"""Вставляет key_to_insert в BST (рекурсивно). Возвращает корень поддерева."""
# Базовый случай: нашли место, создаем узел
if node is None:
return TreeNode(key_to_insert)
# Идем влево или вправо (без вставки дубликатов)
if key_to_insert < node.key:
node.left = insert_bst(node.left, key_to_insert)
elif key_to_insert > node.key:
node.right = insert_bst(node.right, key_to_insert)
# else: ключ уже есть, ничего не делаем
return node # Возвращаем узел (возможно, с обновленным потомком)
# --- Вспомогательная функция для печати (In-order) ---
def get_inorder_keys(node):
return get_inorder_keys(node.left) + [node.key] + get_inorder_keys(node.right) if node else []
bst_root = None
keys_to_insert = [50, 30, 70, 20, 40, 60, 80, 35]
print(f"--- Вставка в BST ---") # Оставим для ясности
print(f"Вставляем ключи: {keys_to_insert}")
for key in keys_to_insert:
bst_root = insert_bst(bst_root, key) # Переприсваиваем корень
print(f"Результат (In-order): {get_inorder_keys(bst_root)}")
# [20, 30, 35, 40, 50, 60, 70, 80]Структура получившегося дерева:
50
/ \
30 70
/ \ / \
20 40 60 80
/
35Аналогично поиску, сложность вставки зависит от высоты дерева:
- Средний случай (сбалансированное дерево): O(log n)
- Худший случай (вырожденное дерево): O(n)
Вставка — одна из основных операций для построения BST. Теперь кратко рассмотрим последнюю базовую операцию — удаление.
Удаление из BST
Удаление узла из бинарного дерева поиска — более хитрая операция, чем вставка или поиск, потому что нам нужно не просто убрать узел, но и перестроить связи так, чтобы основное свойство BST (Левый < Корень < Правый) сохранилось для всего дерева.
Алгоритм удаления обычно рассматривает три случая, в зависимости от того, сколько потомков имеет удаляемый узел:
- Узел-лист (0 потомков). Это самый простой вариант. Достаточно просто удалить ссылку на этот узел у его родителя. Если удаляется корень-лист, дерево становится пустым.
- Узел с 1 потомком. В этом случае мы "обходим" удаляемый узел, напрямую связывая его родителя с его единственным потомком.
- Узел с 2 потомками. Это самый сложный сценарий. Нельзя просто удалить узел. Нужно найти ему "замену". Заменой обычно выступает либо наибольший элемент в левом поддереве (in-order predecessor), либо наименьший элемент в правом поддереве (in-order successor). Затем ключ из узла-замены копируется в удаляемый узел. После этого рекурсивно удаляется сам узел-замена, что сводится к одному из двух предыдущих, более простых случаев (так как у predecessor/successor не может быть двух потомков).
Реализация функции удаления, особенно для случая с двумя потомками, довольно громоздка и требует аккуратной работы со ссылками и рекурсией. Мы не будем приводить её здесь, так как это выходит за рамки базового обзора BST. Главное — понимать концептуальные шаги и три случая.
Как и поиск со вставкой, удаление из BST имеет:
- Среднюю временную сложность O(log n) (для сбалансированных деревьев).
- Худшую временную сложность O(n) (для вырожденных деревьев).
Итого: бинарные деревья роиска предоставляют эффективный способ (в среднем O(log n)) для поиска, вставки и удаления элементов, поддерживая их в упорядоченном состоянии. Однако их производительность сильно зависит от сбалансированности дерева.
Кучи и модуль heapq
Представьте, что вам нужна структура данных, из которой можно очень быстро извлекать самый маленький (или самый большой) элемент. Обычные списки или BST не идеальны для этого: в списке поиск минимума займет O(n), в BST минимум находится быстро (крайний левый узел, O(log n) или O(n)), но основное назначение BST другое.
Здесь на помощь приходит куча (heap). Концептуально, куча — это специализированное бинарное дерево, удовлетворяющее следующим свойствам:
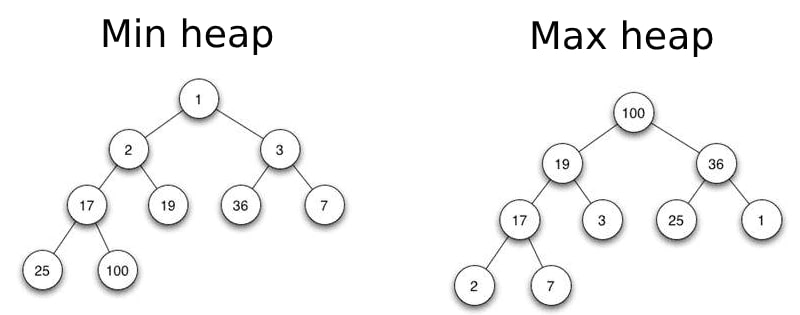
- Min-Heap (минимальная куча): Значение в любом узле меньше или равно значениям его потомков. Корень всегда содержит самый маленький элемент.
- Max-Heap (максимальная куча): Значение в любом узле больше или равно значениям его потомков. Корень всегда содержит самый большой элемент.
Куча обычно является полным или почти полным бинарным деревом, что позволяет эффективно представлять её с помощью обычного списка. Структура дерева и связи поддерживаются через индексы: для элемента `heap[i]`, его дети — `heap[2*i + 1]` и `heap[2*i + 2]`, а родитель — `heap[(i - 1) // 2]`.
Стандартный модуль heapq в Python реализует Min-Heap. Он не использует явные узлы и ссылки, как `TreeNode`. Вместо этого он очень эффективно представляет кучу, используя обычный список, где структура дерева поддерживается математически через индексы:
- Корень находится в `heap[0]`.
- Для узла с индексом `i`, его левый потомок — `heap[2*i + 1]`, правый — `heap[2*i + 2]`.
- Для узла с индексом `i` (кроме корня), его родитель — `heap[(i - 1) // 2]`.
Это позволяет выполнять ключевые операции очень быстро. Основные функции в `heapq` такие:
- `heapq.heappush(heap, item)`: Добавляет `item` в список `heap`, сохраняя свойство кучи. O(log n).
- `heapq.heappop(heap)`: Удаляет и возвращает наименьший элемент (`heap[0]`) из кучи, перестраивая её. O(log n). Вызывает `IndexError`, если куча пуста.
- Доступ к минимуму: Просто `heap[0]` возвращает наименьший элемент без его удаления. O(1).
- `heapq.heapify(list)`: Превращает обычный список в кучу "на месте" (in-place). Делает это за O(n) времени, что эффективнее, чем добавлять элементы по одному (n * log n).
Главное применение:
Куча идеально подходит для реализации очереди с приоритетом (priority queue), где элементы извлекаются не в порядке добавления, а по их приоритету (наименьший приоритет извлекается первым в `min-heap`).
Куча идеально подходит для реализации очереди с приоритетом (priority queue), где элементы извлекаются не в порядке добавления, а по их приоритету (наименьший приоритет извлекается первым в `min-heap`).
import heapq
# Очередь задач: (приоритет, описание). Меньше число = Высший приоритет.
tasks_queue = []
heapq.heappush(tasks_queue, (5, "Low priority task")) # Низкий приоритет
heapq.heappush(tasks_queue, (1, "Urgent bugfix")) # Высший приоритет!
heapq.heappush(tasks_queue, (3, "Write documentation")) # Средний приоритет
heapq.heappush(tasks_queue, (1, "Reply to boss")) # Тоже высший приоритет
print(f"Текущая задача (высший приоритет, без извлечения): {tasks_queue[0]}") # O(1)
print("Обработка задач по приоритету:")
while tasks_queue:
priority, task = heapq.heappop(tasks_queue) # Извлекаем с наименьшим приоритетом O(log n)
print(f" - Приоритет {priority}: Выполняем '{task}'")Трюк для Max-Heap: Чтобы симулировать `max-heap` с помощью `heapq` (который min-heap), храните элементы как кортежи (`-приоритет`, `данные`). `heapq` извлечет элемент с наименьшим отрицательным приоритетом, что соответствует наибольшему положительному исходному приоритету.
Когда использовать heapq?
Когда использовать heapq?
- Реализация очередей с приоритетом.
- Алгоритмы на графах (Дейкстра, Прим).
- Нахождение k наибольших/наименьших элементов (эффективнее, чем полная сортировка).
- Симуляции событий (обработка по времени).
Заключение: деревья покорены!
Эта часть нашего гайда была посвящена деревьям — фундаментальной нелинейной структуре данных, которая позволяет моделировать иерархические отношения.
Деревья — это мощнейший инструмент для представления иерархий и организации данных. Бинарные деревья поиска предлагают эффективный способ работы с упорядоченными данными (O(log n) в среднем), а кучи незаменимы для быстрого доступа к минимальному/максимальному элементу. Понимание различных алгоритмов обхода (DFS, BFS) является ключом к решению множества задач на деревьях.
Мы заложили солидный фундамент для понимания нелинейных структур. Теперь мы готовы перейти к еще более общей и гибкой структуре, способной моделировать самые разнообразные связи между объектами. В Части 6 мы погрузимся в мир графов.
