С возвращением, неутомимые исследователи Python! 🚀 В предыдущих частях мы заложили фундамент (Часть 1: Встроенный Арсенал) и расширили инструментарий специализированными структурами вроде deque и концептуально важными связанными списками (Часть 2: Deque и Linked Lists). Мы много говорили о том, как хранить данные. Теперь пришло время сместить фокус на то, как решать задачи, используя продвинутые техники программирования.
Весь маршрут нашего гайда:
Понимание этих техник не только расширит ваш арсенал для алгоритмических задач и собеседований, но и поможет писать более продуманный код в реальных проектах.
Поехали! 🚀
- Часть 1: базовый арсенал.
- Часть 2: стеки, очереди и связанные списки.
- Часть 3 (вы здесь): рекурсия и оптимизация через динамическое программирование.
- Часть 4: алгоритмы поиска и сортировки.
- Часть 5: деревья, BST и heapq.
- Часть 6: графы — моделируем всё, что связано.
Понимание этих техник не только расширит ваш арсенал для алгоритмических задач и собеседований, но и поможет писать более продуманный код в реальных проектах.
Поехали! 🚀
Рекурсия в Python: элегантность, опасности и стек вызовов🌀
Представьте себе матрёшку: чтобы увидеть самую маленькую куколку, вы открываете большую, внутри которой находится кукла поменьше, затем еще меньше, и так далее, пока не дойдете до последней фигурки. Или вообразите два зеркала, стоящие друг напротив друга — вы увидите коридор из отражений, теоретически уходящий в бесконечность.
Это визуальные аналогии рекурсии. В мире программирования рекурсия — это техника, при которой функция вызывает саму себя для решения задачи.
Вместо того чтобы решать проблему "в лоб" одним большим шагом (как часто делают циклы), рекурсивная функция подходит к ней иначе:
Это элегантный способ разбивать сложные проблемы на управляемые части, которые имеют одинаковую структуру, но разный масштаб. Звучит просто и красиво, не так ли? Но, как и у всего мощного, у рекурсии есть свои правила и подводные камни. Чтобы она работала правильно у рекурсивной функции должна быть четкая структура.
Это визуальные аналогии рекурсии. В мире программирования рекурсия — это техника, при которой функция вызывает саму себя для решения задачи.
Вместо того чтобы решать проблему "в лоб" одним большим шагом (как часто делают циклы), рекурсивная функция подходит к ней иначе:
- Она смотрит, можно ли свести текущую задачу к более простой версии той же самой задачи.
- Если да, она делегирует решение этой упрощенной версии... самой себе!
- Этот процесс повторяется, пока задача не упростится до такого состояния, что ее можно решить напрямую, без дальнейших вызовов.
Это элегантный способ разбивать сложные проблемы на управляемые части, которые имеют одинаковую структуру, но разный масштаб. Звучит просто и красиво, не так ли? Но, как и у всего мощного, у рекурсии есть свои правила и подводные камни. Чтобы она работала правильно у рекурсивной функции должна быть четкая структура.
Анатомия рекурсивной функции
Чтобы рекурсия не закончилась всплытием ошибки `RecursionError`, она должна включать два обязательных компонента:
- Базовый случай (base case): Это условие остановки, самый простой вариант задачи, который функция может решить без дальнейших рекурсивных вызовов. Она просто возвращает конкретный результат.
- Рекурсивный шаг (recursive step): Часть, где функция вызывает сама себя. Задача как бы "делегируется" более простому вызову той же функции. Важно, что этот самовызов происходит с измененными аргументами, которые гарантированно приближают нас к базовому случаю.
Наличие обоих этих компонентов критически важно. Базовый случай гарантирует, что процесс когда-нибудь закончится. Рекурсивный шаг гарантирует, что мы движемся к этому базовому случаю.
Чтобы увидеть это в действии, давайте разберем самый хрестоматийный пример рекурсии — вычисление факториала.
Чтобы увидеть это в действии, давайте разберем самый хрестоматийный пример рекурсии — вычисление факториала.
Классика жанра: факториал
Факториал числа `n` (обозначается `n!`) — это произведение всех натуральных чисел от 1 до `n` включительно. То есть, `n! = 1 * 2 * 3 * ... * n`. А факториал нуля равен 1.
Примеры:
Как представить это рекурсивно? Нам нужно найти базовый случай и рекурсивный шаг.
Теперь мы готовы написать рекурсивную функцию:
Примеры:
- 3! = 1 * 2 * 3 = 6
- 4! = 1 * 2 * 3 * 4 = 24
- 1! = 1
- 0! = 1
Как представить это рекурсивно? Нам нужно найти базовый случай и рекурсивный шаг.
- Поиск рекурсивного шага. Давайте посмотрим на `4! = 4 * 3 * 2 * 1`. Мы видим, что `3 * 2 * 1` — это `3!`. Значит, `4! = 4 * 3!`. В общем виде, `n! = n * (n-1)!`. Вот он, рекурсивный шаг! Мы свели вычисление факториала `n` к вычислению факториала `n-1`.
- Поиск базового случая. Наше рекурсивное определение `n! = n * (n-1)!` работает для `n > 1`. А что если `n=1`? Тогда `1! = 1`. А если `n=0`? По определению, `0! = 1`. Эти случаи не требуют дальнейшего умножения или вызова факториала от меньшего числа. Это и есть наши базовые случаи, точки остановки. Мы можем объединить их: если n равно 0 или 1, результат равен 1.
Теперь мы готовы написать рекурсивную функцию:
def factorial_recursive(n):
"""Вычисляет факториал n с помощью рекурсии."""
# Добавим выводы, чтобы видеть процесс
print(f"Вычисляем factorial_recursive({n})...")
# Сначала проверим корректность ввода
if not isinstance(n, int) or n < 0:
raise ValueError("Факториал определен только для целых неотрицательных чисел")
# 1. Базовый случай
if n == 0 or n == 1:
print(f"Базовый случай для n={n}, возвращаем 1.")
return 1
# 2. Рекурсивный шаг
else:
print(f"Рекурсивный шаг для n={n}. Вызываем factorial_recursive({n-1}).")
# Вызываем себя же для n-1
result_n_minus_1 = factorial_recursive(n - 1)
# Комбинируем результат
result = n * result_n_minus_1
print(f"Вернулись к n={n}. Результат {n} * factorial({n-1}) = {result}")
return result
# --- Пример вызова ---
try:
target_n = 4
print(f"\n--- Запускаем вычисление {target_n}! ---")
final_result = factorial_recursive(target_n)
print(f"--- Готово ---")
print(f"\nИтоговый факториал {target_n}! = {final_result}")
except ValueError as e:
print(f"Ошибка: {e}")
# Попробуем некорректный ввод
try:
print("\n--- Пробуем factorial_recursive(-1) ---")
factorial_recursive(-1)
except ValueError as e:
print(f"Ожидаемая ошибка: {e}")Давайте проследим за выводом при вызове `factorial_recursive(4)`:
--- Запускаем вычисление 4! ---
Вычисляем factorial_recursive(4)...
Рекурсивный шаг для n=4. Вызываем factorial_recursive(3).
Вычисляем factorial_recursive(3)...
Рекурсивный шаг для n=3. Вызываем factorial_recursive(2).
Вычисляем factorial_recursive(2)...
Рекурсивный шаг для n=2. Вызываем factorial_recursive(1).
Вычисляем factorial_recursive(1)...
Базовый случай для n=1, возвращаем 1.
Вернулись к n=2. Результат 2 * factorial(1) = 2
Вернулись к n=3. Результат 3 * factorial(2) = 6
Вернулись к n=4. Результат 4 * factorial(3) = 24
--- Готово ---
Итоговый факториал 4! = 24
--- Пробуем factorial_recursive(-1) ---
Вычисляем factorial_recursive(-1)...
Ожидаемая ошибка: Факториал определен только для целых неотрицательных чиселМы видим, как функция последовательно вызывает себя с уменьшающимся `n`, пока не доходит до базового случая `(n=1)`, после чего результаты начинают "возвращаться" и умножаться на каждом уровне, пока не будет получен финальный ответ для `n=4`.
Но как Python умудряется отслеживать все эти вложенные вызовы и помнить, куда возвращать результат? Для этого существует специальный механизм — стек вызовов.
Но как Python умудряется отслеживать все эти вложенные вызовы и помнить, куда возвращать результат? Для этого существует специальный механизм — стек вызовов.
За кулисами: стек вызовов
Как Python умудряется не запутаться во всех этих вложенных вызовах? С помощью специальной структуры данных, которая называется стек вызовов (Call Stack).
Мы уже знакомы с концепцией стека (LIFO - Last-In, First-Out) из предыдущей части, когда обсуждали `collections.deque`. Стек вызовов работает точно по такому же принципу.
Каждый раз, когда вызывается функция (неважно, обычная или рекурсивная), для нее создается специальная запись — фрейм стека (stack frame). Этот фрейм содержит всю важную информацию об этом конкретном вызове: значения аргументов, с которыми функция была вызвана; локальные переменные этой функции; а также адрес возврата — то есть место в коде, куда нужно вернуться после завершения работы этой функции.
Этот фрейм помещается на вершину стека вызовов (операция `push`). Если эта функция, в свою очередь, вызывает другую функцию (или саму себя), процесс повторяется: создается новый фрейм для нового вызова и кладется поверх предыдущего.
Когда функция завершает свою работу (доходит до оператора return или просто до конца своего кода), ее фрейм снимается с вершины стека (операция `pop`). После этого управление передается обратно по адресу возврата, который был сохранен во фрейме, лежащем теперь на вершине стека (то есть в ту функцию, которая и вызвала только что завершившуюся).
Мы уже знакомы с концепцией стека (LIFO - Last-In, First-Out) из предыдущей части, когда обсуждали `collections.deque`. Стек вызовов работает точно по такому же принципу.
Каждый раз, когда вызывается функция (неважно, обычная или рекурсивная), для нее создается специальная запись — фрейм стека (stack frame). Этот фрейм содержит всю важную информацию об этом конкретном вызове: значения аргументов, с которыми функция была вызвана; локальные переменные этой функции; а также адрес возврата — то есть место в коде, куда нужно вернуться после завершения работы этой функции.
Этот фрейм помещается на вершину стека вызовов (операция `push`). Если эта функция, в свою очередь, вызывает другую функцию (или саму себя), процесс повторяется: создается новый фрейм для нового вызова и кладется поверх предыдущего.
Когда функция завершает свою работу (доходит до оператора return или просто до конца своего кода), ее фрейм снимается с вершины стека (операция `pop`). После этого управление передается обратно по адресу возврата, который был сохранен во фрейме, лежащем теперь на вершине стека (то есть в ту функцию, которая и вызвала только что завершившуюся).
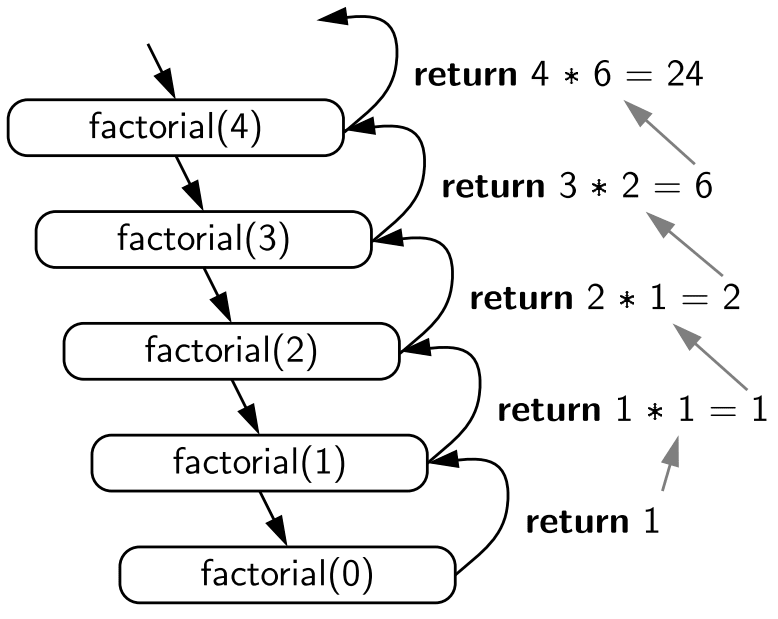
Механизм стека LIFO идеально подходит для управления вложенными вызовами функций, обеспечивая правильный порядок возврата управления и результатов. Однако именно этот механизм и накладывает на рекурсию существенные ограничения.
Плюсы и минусы рекурсии ⚖️
Рекурсия — мощный инструмент, но, как и любой инструмент, она имеет свои сильные и слабые стороны.
👍 Плюсы рекурсии
- Элегантность и читаемость (для подходящих задач). Для задач, которые по своей природе рекурсивны (например, работа с древовидными структурами данных, фракталами, математическими определениями типа факториала или чисел Фибоначчи), рекурсивный код часто получается значительно короче, чище и понятнее, чем итеративный аналог. Итеративное решение может потребовать сложных циклов, дополнительных переменных для хранения промежуточного состояния и быть менее очевидным.
- Близость к математическим определениям. Многие математические функции и последовательности имеют естественное рекурсивное определение. Рекурсия позволяет перевести такие определения в код почти один к одному, что упрощает разработку и проверку корректности.
- Решение сложных задач. Некоторые сложные задачи, особенно связанные с обходом или генерацией комбинаторных объектов (например, в алгоритмах поиска с возвратом - backtracking), гораздо проще реализовать с помощью рекурсии.
👎 Минусы рекурсии (особенно в Python)
- Накладные расходы на вызов функций. Каждый вызов функции, включая рекурсивный, — это не бесплатная операция. Требуется время на создание фрейма стека, передачу аргументов, сохранение состояния и возврат управления. Из-за этого рекурсивное решение почти всегда медленнее, чем эквивалентное итеративное решение, использующее циклы.
- Ограничение глубины стека. Вот она, главная опасность! У стека вызовов есть физический предел размера. Если рекурсия "погружается" слишком глубоко (то есть происходит слишком много вложенных вызовов до достижения базового случая), стек переполняется, и Python аварийно завершает программу с ошибкой `RecursionError: maximum recursion depth exceeded`. В CPython (стандартной реализации) это ограничение по умолчанию довольно консервативно (часто около 1000 вызовов). Его можно посмотреть (`sys.getrecursionlimit()`) и даже изменить (`sys.setrecursionlimit()`), но делать это нужно с большой осторожностью и пониманием последствий, так как это может привести к еще более серьезным сбоям (например, к падению интерпретатора из-за нехватки памяти).
- Потребление памяти. Каждый фрейм в стеке вызовов занимает память. Глубокая рекурсия может "съесть" значительный объем оперативной памяти, особенно если фреймы содержат много данных.
- Сложность отладки. Отслеживать поток выполнения и состояние переменных через множество рекурсивных вызовов может быть значительно сложнее, чем отлаживать линейный итеративный код. Понять, на каком уровне рекурсии что-то пошло не так, бывает непросто.
Когда использовать рекурсию?
Учитывая плюсы и минусы, когда же рекурсия является хорошим выбором в Python?
- Когда структура задачи естественно рекурсивна. Классический пример — обход деревьев и графов. Рекурсивные алгоритмы обхода (pre-order, in-order, post-order для деревьев; DFS для графов) часто выглядят намного проще и понятнее итеративных аналогов, использующих явный стек.
- Когда читаемость и простота кода важнее пиковой производительности. Если участок кода не является критичным для производительности всей системы, а рекурсивное решение заметно чище и проще в поддержке, чем итеративное, — это может быть оправданным выбором.
- Когда вы уверены, что глубина рекурсии будет небольшой и гарантированно не превысит лимит стека для всех ожидаемых входных данных.
Важное замечание: Для многих простых задач, которые часто приводят как примеры рекурсии (вроде факториала или чисел Фибоначчи), итеративное решение в Python почти всегда будет более предпочтительным. Оно быстрее, не рискует переполнением стека и часто не сильно сложнее в написании. Рекурсию для таких задач стоит рассматривать скорее как учебный пример.
Теперь, давайте посмотрим, как можно оптимизировать рекурсивные решения, которые страдают от повторных вычислений, с помощью динамического программирования.
Динамическое программирование: оптимизация через память 🧠💾
Представьте, что вас попросили посчитать сумму 2 + 3. Вы посчитали, получили 5. Через минуту вас снова просят посчитать 2 + 3. Вы же не будете снова делать расчёт? Вы просто вспомните результат — 5. Динамическое программирование работает по схожему принципу: не решай одну и ту же задачу дважды!
Давайте рассмотрим классическую задачу, где наивная рекурсия показывает себя во всей "красе" неэффективности — вычисление чисел Фибоначчи. Напомню, последовательность Фибоначчи определяется так: `fib(n) = fib(n-1) + fib(n-2)`, а `fib(0)=0, fib(1)=1`.
Рекурсивная функция, написанная "в лоб" по этому определению, выглядит так:
# КРАЙНЕ НЕЭФФЕКТИВНАЯ наивная рекурсия для Фибоначчи
def fib_naive(n):
# print(f"Вычисляем fib_naive({n})") # Раскомментируйте, чтобы увидеть лавину вызовов
if n < 0:
raise ValueError("N должно быть >= 0")
if n <= 1:
return n
else:
# Вот здесь проблема: fib(n-1) и fib(n-2) будут многократно
# вызывать вычисление ОДНИХ И ТЕХ ЖЕ меньших значений fib(k)
return fib_naive(n - 1) + fib_naive(n - 2)
# --- Попробуем вызвать (даже для небольшого n) ---
import time
n_val = 40 # Уже достаточно, чтобы увидеть тормоза
print(f"Вычисляем fib({n_val}) наивной рекурсией (может занять время)...")
start_time = time.perf_counter()
try:
result_naive = fib_naive(n_val)
end_time = time.perf_counter()
print(f"fib({n_val}) = {result_naive}")
print(f"Время выполнения: {end_time - start_time:.6f} сек")
except ValueError as e:
print(e)
except RecursionError:
print("Ошибка: Достигнута максимальная глубина рекурсии!")Если вы запустите этот код, например, для `n = 40`, то заметите, что он работает весьма медленно. Почему?
Давайте посмотрим на дерево вызовов для `fib_naive(5)`:
Давайте посмотрим на дерево вызовов для `fib_naive(5)`:
fib(5)
/ \
fib(4) fib(3) <-- fib(3) вызывается 1 раз здесь
/ \ / \
fib(3) fib(2) fib(2) fib(1) <-- fib(3) вызывается еще 1 раз, fib(2) - 2 раза
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0) <-- fib(2) вызывается еще раз...
/ \
fib(1) fib(0)Видно, что `fib(3)` вычисляется 2 раза, `fib(2)` — 3 раза, `fib(1)` — 5 раз! Количество вызовов растет экспоненциально (примерно как O(2^n)). Для `fib(40)` количество операций становится очень большим.
Эта проблема возникает из-за перекрывающихся подзадач (overlapping subproblems): при решении большой задачи (`fib(n)`) нам многократно приходится решать одни и те же подзадачи меньшего размера (`fib(k)` для `k < n`).
Эта проблема возникает из-за перекрывающихся подзадач (overlapping subproblems): при решении большой задачи (`fib(n)`) нам многократно приходится решать одни и те же подзадачи меньшего размера (`fib(k)` для `k < n`).
Основная идея ДП: запомни и переиспользуй! 💡
Динамическое программирование предлагает простое решение: если мы уже решили какую-то подзадачу, давайте запомним её результат. Если эта же подзадача встретится нам снова, мы просто возьмем готовый ответ из "памяти", а не будем вычислять его заново.
Этот процесс "запоминания" позволяет кардинально снизить количество вычислений. Для Фибоначчи, например, сложность упадет с экспоненциальной O(2^n) до линейной O(n), потому что каждое значение `fib(k)` будет реально вычислено только один раз. Это колоссальный выигрыш!
Условия применимости динамического программирования
ДП — это не универсальный метод, он подходит для задач, обладающих двумя ключевыми свойствами:
- Перекрывающиеся подзадачи (overlapping subproblems). Как мы видели на примере Фибоначчи, задача должна разбиваться на подзадачи, которые многократно переиспользуются при решении исходной задачи. Если все подзадачи уникальны (как, например, в сортировке слиянием), то ДП не даст выигрыша.
- Оптимальная подструктура (optimal substructure). Оптимальное решение исходной задачи должно быть возможно построить из оптимальных решений ее подзадач. Для Фибоначчи это выполняется: чтобы найти оптимальное (единственно верное) `fib(n)`, нам нужны оптимальные (верные) `fib(n-1)` и `fib(n-2)`. Это свойство характерно для многих оптимизационных задач (например, поиск кратчайшего пути, задача о рюкзаке).
Если оба эти свойства присутствуют, то динамическое программирование — ваш кандидат номер один для эффективного решения.
Существует два классических подхода к реализации ДП: мемоизация (сверху-вниз) и табуляция (снизу-вверх). Давайте рассмотрим их по порядку.
Мемоизация (memoization): рекурсия с кешем (сверху-вниз / Top-Down) 🧠
Мемоизация — это, по сути, умная рекурсия. Мы сохраняем основную рекурсивную логику решения задачи "сверху вниз" (от большой задачи к маленьким), но добавляем кеш (cache) или "памятку" (memo), чтобы хранить результаты уже решенных подзадач.
Как это работает:
- Инициализация кеша. Перед началом вычислений создается структура для хранения результатов (обычно это словарь dict или массив/список list, если аргументы — последовательные целые числа).
- Проверка кеша. В самом начале рекурсивной функции мы проверяем: "Есть ли результат для текущих аргументов уже в нашем кеше?". Если да — ура! Мы немедленно возвращаем сохраненное значение, избегая лишних вычислений.
- Базовый случай. Если результата в кеше нет, проверяем, не достигли ли мы базового случая рекурсии. Если да — возвращаем результат базового случая (и, опционально, сохраняем его в кеш).
- Рекурсивное вычисление. Если это не базовый случай и результата в кеше нет, мы выполняем рекурсивный шаг: вызываем функцию для подзадач и комбинируем их результаты, чтобы получить решение для текущей задачи.
- Сохранение в кеш. Перед тем как вернуть только что вычисленный результат, мы сохраняем его в кеш, ассоциируя с текущими аргументами.
- Возврат результата. Возвращаем вычисленный (и теперь сохраненный) результат.
Пример: Фибоначчи с мемоизацией
Давайте применим этот алгоритм к нашей функции `fib_naive`:
# Кеш для хранения уже вычисленных значений fib(k)
# Используем словарь, так как ключи (n) могут быть любыми (хотя здесь целые)
memo_fib = {}
def fib_memo(n):
"""Вычисляет числа Фибоначчи с использованием мемоизации (явный кеш)."""
# print(f"Попытка вычислить fib_memo({n})")
if n < 0:
raise ValueError("N должно быть >= 0")
# 1. Проверка кеша
if n in memo_fib:
# print(f" Нашли fib({n})={memo_fib[n]} в кеше!")
return memo_fib[n]
# 2. Базовый случай
if n <= 1:
result = n
# 3. Рекурсивный шаг (если не в кеше и не базовый случай)
else:
# print(f" Вычисляем fib({n}) = fib({n-1}) + fib({n-2})")
result = fib_memo(n - 1) + fib_memo(n - 2)
# 4. Сохранение в кеш ПЕРЕД возвратом
# print(f" Сохраняем fib({n}) = {result} в кеш")
memo_fib[n] = result
# 5. Возврат
return result
# --- Вызов ---
import time
n_val = 40 # То же значение, что было медленным раньше
print(f"\n--- Вычисляем fib({n_val}) с мемоизацией ---")
start_time = time.perf_counter()
result_memo = fib_memo(n_val)
end_time = time.perf_counter()
print(f"fib({n_val}) = {result_memo}")
print(f"Время выполнения: {end_time - start_time:.6f} сек") # Теперь это МГНОВЕННО!
# Посмотрим на кеш после вычислений (для интереса)
# print(f"\nСодержимое кеша memo_fib после вычисления fib({n_val}):")
# print(memo_fib)
# Повторный вызов будет еще быстрее, т.к. все уже в кеше
print(f"\n--- Повторный вызов fib({n_val}) ---")
start_time = time.perf_counter()
result_memo_again = fib_memo(n_val)
end_time = time.perf_counter()
print(f"fib({n_val}) = {result_memo_again}")
print(f"Время выполнения повторного вызова: {end_time - start_time:.6f} сек")Теперь вычисление `fib(40)` (и даже `fib(100)`) происходит практически мгновенно! Каждый `fib(k)` вычисляется только один раз. Временная сложность упала с O(2^n) до O(n), так как нам нужно вычислить каждое значение от `fib(0)` до `fib(n)` ровно по одному разу. Пространственная сложность стала O(n) из-за хранения кеша и глубины рекурсивного стека.
Pythonic Way: встроенная Мемоизация с functools ✨
Писать логику кеширования вручную каждый раз? Не по-питоновски! К счастью, в стандартной библиотеке functools есть волшебные декораторы, которые делают всю грязную работу за нас:
Давайте перепишем Фибоначчи с использованием `@cache`:
- `@functools.lru_cache(maxsize=...)`. Этот декоратор автоматически кеширует результаты вызовов функции. `maxsize` задает максимальное количество результатов, которые будут храниться в кеше. Когда кеш заполнен, используется стратегия LRU (Least Recently Used) — наименее используемые результаты вытесняются новыми. Если `maxsize=None`, кеш неограничен.
- `@functools.cache` (доступен с Python 3.9+)/ Более простой и современный синтаксис для создания неограниченного кеша. Эквивалентен `@lru_cache(maxsize=None)`.
Давайте перепишем Фибоначчи с использованием `@cache`:
import functools
import time
# import sys
# При необходимости можно увеличить лимит рекурсии, но кеш часто помогает
# sys.setrecursionlimit(2000)
# Используем декоратор @cache (для Python 3.9+)
# или @functools.lru_cache(maxsize=None) для более старых версий
@functools.cache
def fib_cached(n):
"""Вычисляет Фибоначчи с автоматической мемоизацией через @cache."""
# print(f"Вызов fib_cached({n})") # Можно раскомментировать для отладки
if n < 0:
raise ValueError("N должно быть >= 0")
if n <= 1:
return n
else:
return fib_cached(n - 1) + fib_cached(n - 2)
# --- Вызов ---
n_val_cache = 100 # Теперь можно брать n побольше!
print(f"\n--- Вычисляем fib({n_val_cache}) с @cache ---")
start_time = time.perf_counter()
result_cache = fib_cached(n_val_cache)
end_time = time.perf_counter()
print(f"fib({n_val_cache}) = {result_cache}")
print(f"Время выполнения: {end_time - start_time:.6f} сек")
# Декоратор предоставляет удобный способ посмотреть статистику кеша
print(f"Статистика кеша fib_cached: {fib_cached.cache_info()}")
# Вывод может быть: CacheInfo(hits=98, misses=101, maxsize=None, currsize=101)
# hits - сколько раз результат взят из кеша
# misses - сколько раз результат пришлось вычислить
# currsize - текущий размер кешаИспользование декораторов `@cache` или `@lru_cache` — это идиоматичный и предпочтительный способ реализации мемоизации в Python. Код остается чистым и сфокусированным на рекурсивной логике, а кеширование происходит автоматически.
Важный момент: мемоизация решает проблему повторных вычислений, но она не устраняет фундаментальное ограничение рекурсии — глубину стека вызовов. Хотя кеширование часто помогает избежать RecursionError (потому что ветки вызовов для уже вычисленных значений не разворачиваются), для задач с очень большой естественной глубиной рекурсии (даже если нет перекрывающихся подзадач) вы все равно можете столкнуться с этим лимитом.
А что если мы хотим полностью избавиться от рекурсии и связанных с ней ограничений стека? Тут на сцену выходит второй подход к ДП — табуляция.
Табуляция (tabulation) — итерация снизу-вверх (Bottom-Up)📈
В отличие от мемоизации, которая решает задачу "сверху вниз" (от `n` к базовым случаям), табуляция использует итеративный подход "снизу вверх". Мы начинаем с самых маленьких подзадач (базовых случаев) и постепенно, шаг за шагом, вычисляем решения для все больших подзадач, пока не дойдем до той, которая нам нужна. Результаты мы сохраняем в таблице (обычно это массив или список в Python), чтобы использовать их на следующих шагах.
Как это работает (алгоритм):
Как это работает (алгоритм):
- Создание Таблицы. Определяем размер необходимой таблицы (например, `dp_table`) для хранения результатов всех подзадач от базовых до искомой. Создаем эту таблицу (часто заполняя ее нулями или другими маркерами).
- Заполнение базовых случаев. Заполняем ячейки таблицы, соответствующие базовым случаям задачи, известными значениями.
- Итеративное вычисление. Запускаем цикл (или несколько циклов), который проходит по подзадачам в порядке их возрастания (от базовых к большим). На каждом шаге вычисляем решение для текущей подзадачи i, используя уже вычисленные и сохраненные в таблице значения для меньших подзадач (`dp_table[i-1]`, `dp_table[i-2]` и т.д., в зависимости от формулы перехода). Сохраняем результат в `dp_table[i]`.
- Возврат результата. После завершения цикла искомый результат будет находиться в соответствующей ячейке таблицы (например, `dp_table[n]`).
Пример: Фибоначчи с табуляцией
Давайте применим этот итеративный подход к числам Фибоначчи:
import time
def fib_tab(n):
"""Вычисляет числа Фибоначчи с помощью табуляции (используя список)."""
if n < 0:
raise ValueError("N должно быть >= 0")
# Для n=0 и n=1 результат равен n
if n <= 1:
return n
# Шаг 1: Создаем таблицу (список) размером n+1
# dp_table[i] будет хранить значение fib(i)
dp_table = [0] * (n + 1)
# Шаг 2: Заполняем базовые случаи
# dp_table[0] уже 0
dp_table[1] = 1
# Шаг 3: Итеративно вычисляем остальные значения
# Начинаем с i=2, так как 0 и 1 уже известны
for i in range(2, n + 1):
# Используем уже вычисленные значения из таблицы!
dp_table[i] = dp_table[i - 1] + dp_table[i - 2]
# print(f"Рассчитали dp_table[{i}] = {dp_table[i]}") # Для отладки
# Шаг 4: Результат находится в последней ячейке
return dp_table[n]
# --- Вызов ---
n_val_tab = 100 # То же значение, что и для @cache
print(f"\n--- Вычисляем fib({n_val_tab}) с табуляцией ---")
start_time = time.perf_counter()
result_tab = fib_tab(n_val_tab)
end_time = time.perf_counter()
print(f"fib({n_val_tab}) = {result_tab}")
print(f"Время выполнения: {end_time - start_time:.6f} сек") # Тоже очень быстро!Табуляция, как и мемоизация, дает нам линейную временную сложность O(n), что значительно лучше экспоненциальной. В этом варианте мы использовали список dp_table размером `n+1`, поэтому пространственная сложность (память) тоже O(n).
Оптимизация памяти при табуляции
Часто при табуляции можно заметить, что для вычисления текущего значения `dp_table[i]` нам нужны только несколько предыдущих значений (например, `dp_table[i-1]` и `dp_table[i-2]`), а вся остальная часть таблицы уже не используется. В таких случаях можно оптимизировать использование памяти, храня только те немногие предыдущие значения, которые действительно нужны для следующего шага, вместо всей таблицы.
Для чисел Фибоначчи нам нужно помнить только два предыдущих числа. Давайте реализуем это:
import time
def fib_tab_optimized(n):
"""Вычисляет Фибоначчи с табуляцией и оптимизацией памяти до O(1)."""
if n < 0:
raise ValueError("N должно быть >= 0")
if n <= 1:
return n
# Храним только два последних вычисленных значения
prev2 = 0 # Соответствует fib(i-2), начинаем с fib(0)
prev1 = 1 # Соответствует fib(i-1), начинаем с fib(1)
# Итерируемся от 2 до n
for i in range(2, n + 1):
# Вычисляем текущее значение fib(i)
current = prev1 + prev2
# Сдвигаем значения для следующей итерации:
# то, что было prev1, станет prev2
# то, что было current, станет prev1
prev2 = prev1
prev1 = current
# print(f"Итерация {i}: current=fib({i})={current}, prev1={prev1}, prev2={prev2}")
# После завершения цикла prev1 будет содержать fib(n)
return prev1
# --- Вызов ---
n_val_opt = 100
print(f"\n--- Вычисляем fib({n_val_opt}) с оптимизированной табуляцией ---")
start_time = time.perf_counter()
result_opt = fib_tab_optimized(n_val_opt)
end_time = time.perf_counter()
print(f"fib({n_val_opt}) = {result_opt}")
print(f"Время выполнения: {end_time - start_time:.6f} сек") # Быстро, O(n) по времени
print("Пространственная сложность: O(1)") # Используем константное количество памяти!Эта оптимизированная версия по-прежнему работает за O(n) времени, но теперь использует всего O(1) (константное количество) памяти, независимо от n. Это значительное улучшение по сравнению с O(n) памяти в базовой табуляции или потенциально O(n) памяти на стек вызовов в мемоизации.
Теперь, когда мы рассмотрели оба подхода — мемоизацию и табуляцию — давайте сравним их и поймем, когда какой лучше выбрать.
Теперь, когда мы рассмотрели оба подхода — мемоизацию и табуляцию — давайте сравним их и поймем, когда какой лучше выбрать.
Мемоизация vs табуляция: битва подходов ⚔️
Выбор между мемоизацией и табуляцией часто зависит от специфики задачи, стиля программирования и требований к производительности/памяти. Вот ключевые различия:
Ко
Мемоизация может быть предпочтительнее, если пространство состояний (количество возможных подзадач) очень велико, но для получения конкретного ответа нужно вычислить лишь малую его часть, так как она вычислит только необходимое. Она также проще, если вы мыслите рекурсивно или уже имеете рекурсивное решение, особенно с учетом удобства декораторов. Однако ее стоит использовать, если вы уверены, что глубина рекурсии не вызовет RecursionError.
Табуляция является лучшим выбором, если вам нужно вычислить значения для всех подзадач до n. Она надежнее для задач, где рекурсия может быть очень глубокой, так как исключает RecursionError. Часто она дает небольшое преимущество в скорости. И, что очень важно, табуляция является единственным вариантом, если требуется существенная оптимизация памяти, что невозможно при рекурсивных вызовах мемоизации.
В конечном счете, оба подхода приводят к правильному и (обычно) асимптотически одинаковому по времени решению. Для многих задач выбор — это вопрос личных предпочтений и удобства реализации. Однако знание обоих методов и их особенностей позволяет выбрать наиболее подходящий инструмент для конкретной ситуации.
Табуляция является лучшим выбором, если вам нужно вычислить значения для всех подзадач до n. Она надежнее для задач, где рекурсия может быть очень глубокой, так как исключает RecursionError. Часто она дает небольшое преимущество в скорости. И, что очень важно, табуляция является единственным вариантом, если требуется существенная оптимизация памяти, что невозможно при рекурсивных вызовах мемоизации.
В конечном счете, оба подхода приводят к правильному и (обычно) асимптотически одинаковому по времени решению. Для многих задач выбор — это вопрос личных предпочтений и удобства реализации. Однако знание обоих методов и их особенностей позволяет выбрать наиболее подходящий инструмент для конкретной ситуации.
Заключение: рекурсия и ДП — мощные инструменты в вашем арсенале 🚀
Третья часть нашего гайда подошла к концу, мы перешли от структур данных к мощным техникам решения задач.
Ключевой вывод
Рекурсия — это элегантный способ мышления о задачах, сводя их к более простым версиям самих себя, но ее нужно использовать с умом, помня о стеке вызовов. Динамическое Программирование — это не конкретный алгоритм, а мощная методология оптимизации, которая (через мемоизацию или табуляцию) позволяет превратить экспоненциально медленные решения в быстрые полиномиальные, если задача обладает свойствами перекрывающихся подзадач и оптимальной подструктуры.
Теперь в вашем арсенале есть не только разнообразные контейнеры для данных, но и продвинутые подходы к разработке самих алгоритмов. Вы можете не только выбрать правильную структуру, но и написать эффективный код для ее обработки.
В следующей части мы погрузимся в мир классических алгоритмов, которые должен знать каждый разработчик.
В следующей части мы погрузимся в мир классических алгоритмов, которые должен знать каждый разработчик.
