Линейная регрессия — один из базовых инструментов машинного обучения. Она проста, интерпретируема и эффективна, когда зависимость между признаками и целевой переменной близка к (внезапно!) линейной. Однако на практике данные часто демонстрируют более сложные, криволинейные взаимосвязи. Как нам их учитывать?
Один из самых простых способов — полиномиальная регрессия. Мы берем возможности линейной регрессии и расширяем их, позволяя модели "изгибаться" для лучшего соответствия данным. Делается это путем добавления степеней исходных признаков (`x²`, `x³`, ...) в модель. Несмотря на это, в основе своей она использует тот же математический аппарат, что и линейная регрессия, что делает её относительно простой для понимания и реализации.
Что такое полиномиальная регрессия?
Когда простая прямая линия не может адекватно описать зависимость в данных, полиномиальная регрессия предлагает более гибкий подход. Её суть — расширение линейной модели путем добавления новых признаков, которые являются степенями и/или произведениями (взаимодействиями) исходных признаков.
Вспомним уравнение простой линейной регрессии для одного признака `x`:
Вспомним уравнение простой линейной регрессии для одного признака `x`:
y = β₀ + β₁x + εПолиномиальная регрессия берёт эту идею и расширяет ее.
Если у нас есть один исходный признак x, мы добавляем его степени: `x²` (x в квадрате), `x³` (x в кубе) и так далее, до некоторой степени `n`. Уравнение полиномиальной регрессии степени `n` для одного признака выглядит так:
Если у нас есть один исходный признак x, мы добавляем его степени: `x²` (x в квадрате), `x³` (x в кубе) и так далее, до некоторой степени `n`. Уравнение полиномиальной регрессии степени `n` для одного признака выглядит так:
y = β₀ + β₁x + β₂x² + β₃x³ + ... + βₙxⁿ + εА если у нас несколько признаков (`x₁`, `x₂`, ...), то помимо степеней каждого признака (`x₁²`, `x₂²`, и т.д.), которые улавливают нелинейность по каждой оси, мы также добавляем их перекрестные произведения (взаимодействия), такие как `x₁*x₂`, `x₁²*x₂`, `x₁*x₂²` и т.д., вплоть до суммарной степени `n`. Например, для двух признаков (`x₁`, `x₂`) и степени `n=2`, уравнение будет включать:
y = β₀ + β₁x₁ + β₂x₂ + β₃x₁² + β₄x₂² + β₅(x₁*x₂) + εЭти взаимодействия позволяют модели учесть ситуации, когда эффект одного признака (`x₁`) на целевую переменную (`y`) зависит от значения другого признака (`x₂`). Без члена взаимодействия модель предполагает, что эффект `x₁` всегда одинаков, независимо от `x₂`. Это делает модель значительно более гибкой в многомерном пространстве.
Пример: `degree=3`, входной признак `x`(один столбец): `[[2], [3], [4]]`.
Создав полиномы, мы получим три столбца: `x`, `x²`, `x³`:
Создав полиномы, мы получим три столбца: `x`, `x²`, `x³`:
[[ 2, 4, 8],
[ 3, 9, 27],
[ 4, 16, 64]]Пример: degree=2, входные признаки `x₁`, `x₂` (два столбца): `[[a, b], [c, d]]` (`a`, `c` - значения `x₁`; `b`, `d` - значения `x₂`).
Создав полиномы, мы получим пять столбцов: `x₁`, `x₂`, `x₁²`, `x₁*x₂`, `x₂²`:
Создав полиномы, мы получим пять столбцов: `x₁`, `x₂`, `x₁²`, `x₁*x₂`, `x₂²`:
[[a, b, a², a*b, b²],
[c, d, c², c*d, d²]]А теперь вспомним уравнение полиномиальной регрессии, например, для двух признаков и `n=2`:
y = β₀ + β₁x₁ + β₂x₂ + β₃x₁² + β₄x₂² + β₅(x₁*x₂) + εЕсли мы теперь мысленно переобозначим наши признаки:
- `z₁ = x₁`
- `z₂ = x₂`
- `z₃ = x₁²`
- `z₄ = x₂²`
- `z₅ = x₁*x₂`
То уравнение превращается в:
y = β₀ + β₁z₁ + β₂z₂ + β₃z₃ + β₄z₄ + β₅z₅ + εЭто не что иное, как уравнение обычной множественной линейной регрессии!
Зависимость `y` от исходных `x` стала нелинейной. Но зависимость `y` от набора новых признаков (`z₁`, `z₂`, `z₃`, ...) остается линейной. Модель линейна относительно коэффициентов `β`.
Именно поэтому для обучения полиномиальной регрессии (т.е. нахождения оптимальных `β`) мы используем те же методы, что и для обычной линейной регрессии, чаще всего — метод наименьших квадратов (OLS). Алгоритм просто работает с расширенной матрицей признаков, которую мы получили после полиномиальной трансформации.
Зависимость `y` от исходных `x` стала нелинейной. Но зависимость `y` от набора новых признаков (`z₁`, `z₂`, `z₃`, ...) остается линейной. Модель линейна относительно коэффициентов `β`.
Именно поэтому для обучения полиномиальной регрессии (т.е. нахождения оптимальных `β`) мы используем те же методы, что и для обычной линейной регрессии, чаще всего — метод наименьших квадратов (OLS). Алгоритм просто работает с расширенной матрицей признаков, которую мы получили после полиномиальной трансформации.
Что это значит на практике?
- Больше гибкости. Каждый добавленный член (`β₂x²`, `β₃x³`, ...) дает нашей модели дополнительную "степень свободы". Если линейная регрессия может провести только прямую, то полиномиальная регрессия степени 2 (квадратичная) может описать параболу, степени 3 (кубическая) — более сложную S-образную кривую, и так далее. Чем выше степень `n`, тем более сложную форму может принять наша регрессионная кривая.
- Трансформация признаков. Ключевой момент заключается в том, что мы не меняем сам метод регрессии. Мы преобразуем наши входные данные. Вместо одного признака `x` мы создаем набор признаков: `x`, `x²`, `x³`, ..., `xⁿ`. А затем мы обучаем обычную линейную регрессию на этом новом, расширенном наборе признаков. Модель ищет оптимальные коэффициенты `β₀`, `β₁`, `β₂`, ..., `βₙ` для этой "линейной" комбинации исходного признака и его степеней.
- Визуальное отличие. На графике это самое заметное различие. Вместо прямой линии, которая может плохо проходить через облако точек, полиномиальная регрессия строит кривую, которая может гораздо лучше описывать данные.
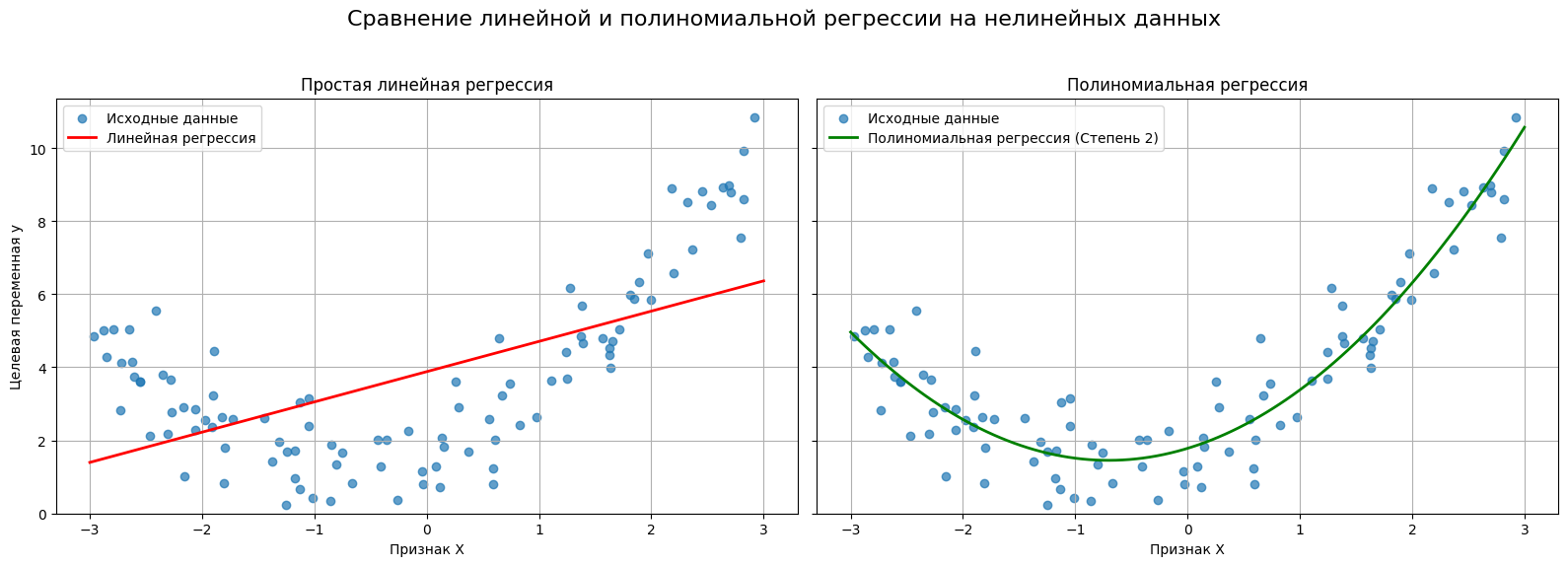
Итог: полиномиальная регрессия — это способ заставить линейную модель работать с нелинейными зависимостями путем добавления новых признаков, основанных на степенях исходных.
Зачем и когда использовать полиномиальную регрессию?
Понимание того, что такое полиномиальная регрессия — это половина дела. Не менее важно знать, когда её применение оправдано и какие проблемы она помогает решить. Ведь не стоит усложнять модель без веской причины.
Итак, в каких случаях стоит задуматься о полиномиальной регрессии?
- Разведочный анализ данных показывает нам нелинейные взаимосвязи. Это самый очевидный и частый сценарий. Когда мы строим точечные графики (scatter plot) для независимой (`X`) и зависимой (`y`) переменных, и точки явно выстраиваются не вдоль прямой, а вдоль некоторой кривой (параболы, S-образной кривой и т.п.), — это является предпосылкой для использования полиномиальной регрессии.
- Сама логика процесса. Иногда понимание предметная область позволяет нам судить о нелинейном характере связи, даже если на необработанных данных это не очевидно из-за шума или специфики выборки.
- Анализ остатков линейной модели. Даже если на первый взгляд зависимость кажется линейной, стоит проверить остатки (residuals) после построения простой линейной модели. Остатки — это разница между фактическими значениями y и значениями, предсказанными моделью (`ŷ = y_actual - y_predicted`). В идеале, если линейная модель хорошо подходит данным, остатки должны быть распределены случайно вокруг нуля, без какого-либо видимого паттерна при построении их зависимости от предсказанных значений (`ŷ`) или от независимой переменной (`X`). Если же на графике остатков вы видите четкую структуру (например, параболу, U-образную форму, или просто систематическое отклонение в разных частях диапазона `X`), это сильный сигнал: линейная модель неспособна уловить всю сложность зависимости, и в данных присутствует нелинейность. Полиномиальная регрессия может помочь это исправить.
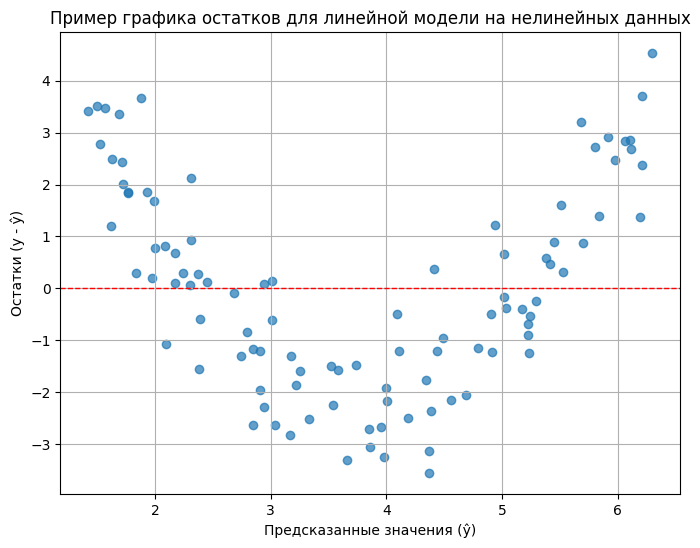
На графике выше остатки явно не случайны. Для средних предсказанных значений (`ŷ`) остатки в основном отрицательные (модель завышает предсказания), а для низких и высоких `ŷ` — в основном положительные (модель занижает предсказания). Этот паттерн — четкий индикатор того, что линейная модель не подходит, и стоит попробовать модель с нелинейными членами, например, полиномиальную регрессию. В идеальном случае точки на графике остатков должны выглядеть как хаотичное облако вокруг красной линии, без выраженных трендов или форм.
Реализация на Python с Scikit-learn
Теория — это хорошо, но давайте посмотрим, как реализовать полиномиальную регрессию с помощью Python.
В качестве примера возьмём набор данных Auto MPG. Он содержит информацию о расходе топлива (в милях на галлон - MPG) для различных моделей автомобилей конца 70-х - начала 80-х годов, а также их характеристики (мощность, вес, количество цилиндров и т.д.). Мы сосредоточимся на зависимости MPG от мощности двигателя (Horsepower), так как она часто демонстрирует нелинейный характер.
В качестве примера возьмём набор данных Auto MPG. Он содержит информацию о расходе топлива (в милях на галлон - MPG) для различных моделей автомобилей конца 70-х - начала 80-х годов, а также их характеристики (мощность, вес, количество цилиндров и т.д.). Мы сосредоточимся на зависимости MPG от мощности двигателя (Horsepower), так как она часто демонстрирует нелинейный характер.
Импорт библиотек и загрузка данных
Сначала импортируем всё необходимое:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures # <--- Ключевой инструмент!
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.pipeline import make_pipeline Затем загрузим датасет из библиотеки `seaborn`.
data = sns.load_dataset('mpg')
display(data.head())
data.info()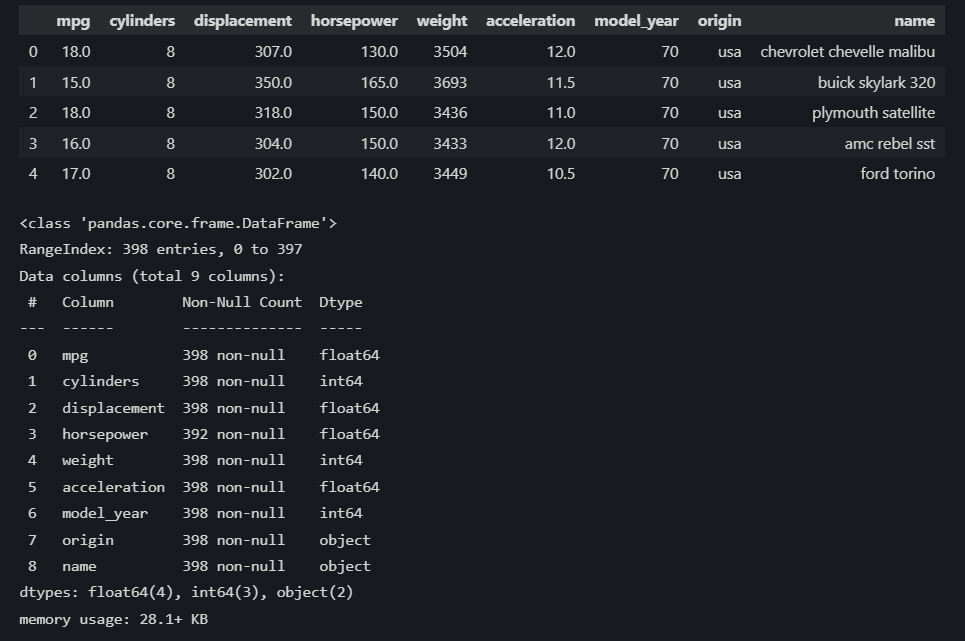
В этом датасете есть пропущенные значения в столбце `horsepower`. Для простоты мы их удалим, но можно использовать и другие способы их обработки.
print(f"\nКоличество пропусков в 'horsepower' до обработки: {data['horsepower'].isnull().sum()}")
data = data.dropna(subset=['horsepower'])
print(f"Количество пропусков в 'horsepower' после удаления: {data['horsepower'].isnull().sum()}")
# Количество пропусков в 'horsepower' до обработки: 6
# Количество пропусков в 'horsepower' после удаления: 0Теперь сформируем наши выборки:
X = data[['horsepower']]
y = data['mpg']
# Разделяем данные на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(f"\nРазмер обучающей выборки: {X_train.shape[0]} записей")
print(f"Размер тестовой выборки: {X_test.shape[0]} записей")
# Размер обучающей выборки: 313 записей
# Размер тестовой выборки: 79 записейВизуализация зависимости
Построим диаграмму рассеяния, чтобы увидеть, как `MPG` зависит от `Horsepower`.
plt.figure(figsize=(10, 6))
sns.scatterplot(x=X_train['horsepower'], y=y_train, alpha=0.7, label='Обучающие данные')
sns.scatterplot(x=X_test['horsepower'], y=y_test, alpha=0.7, label='Тестовые данные', marker='^')
plt.title('Зависимость расхода топлива (MPG) от мощности (Horsepower)')
plt.xlabel('Мощность (Horsepower)')
plt.ylabel('Расход топлива (MPG)')
plt.legend()
plt.grid(True)
plt.show()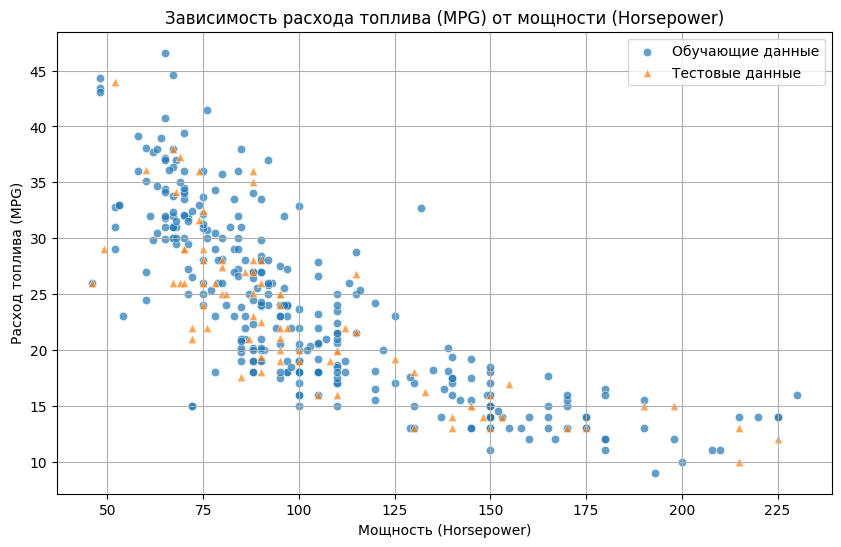
На этом графике точки явно формируют кривую - MPG падает с ростом мощности, но падение замедляется.
Построим простую линейную регрессию
Чтобы оценить пользу от полиномиальной регрессии, сначала применим стандартную линейную модель.
# Обучаем простую линейную регрессию
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
# Делаем предсказания на тестовой выборке
y_lin_pred_test = lin_reg.predict(X_test)
lin_r2 = r2_score(y_test, y_lin_pred_test)
print(f"Линейная регрессия (на тесте): R^2 = {lin_r2:.3f}")
# Линейная регрессия (на тесте): R^2 = 0.566И визуализируем результат:
plt.figure(figsize=(10, 6))
plt.scatter(X['horsepower'], y, alpha=0.6, label='Все данные'
X_plot = np.linspace(X['horsepower'].min(), X['horsepower'].max(), 100).reshape(-1, 1)
y_lin_plot = lin_reg.predict(X_plot)
plt.plot(X_plot, y_lin_plot, color='red', linewidth=2, label=f'Линейная регрессия (R^2={lin_r2:.3f})')
plt.title('Линейная регрессия: MPG vs Horsepower')
plt.xlabel('Мощность (Horsepower)')
plt.ylabel('Расход топлива (MPG)')
plt.legend()
plt.grid(True)
plt.show()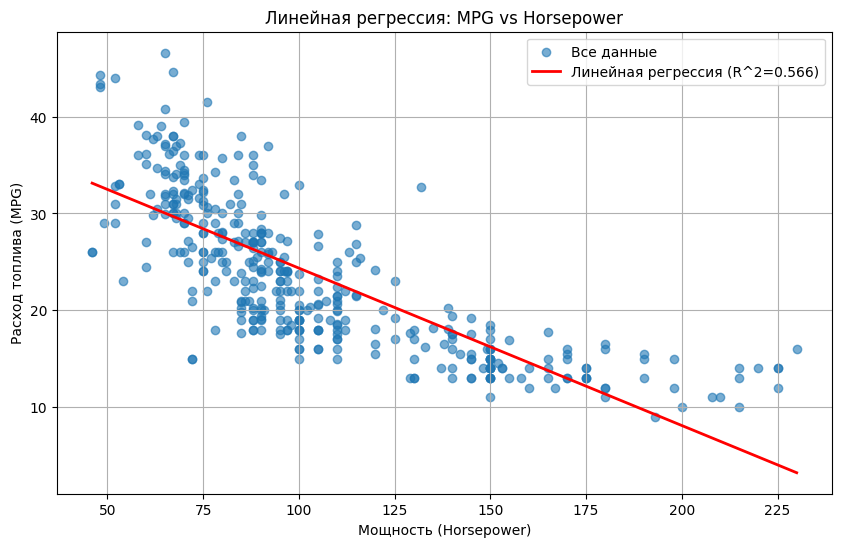
Получаем прямую линию, которая не очень хорошо описывает криволинейный тренд. И R² не очень высокий.
Построим полиномиальную регрессию (второй степени)
Теперь используем `PolynomialFeatures` для создания квадратичного признака (`horsepower²`) и обучим линейную регрессию на расширенном наборе данных. Будем использовать пайплайн для удобства.
degree = 2
poly_reg_pipeline = make_pipeline(
PolynomialFeatures(degree, include_bias=False), # include_bias=False, т.к. LinearRegression добавит свой
LinearRegression()
)
# Обучаем пайплайн на обучающих данных
poly_reg_pipeline.fit(X_train, y_train)
# Делаем предсказания на тестовой выборке
y_poly_pred_test = poly_reg_pipeline.predict(X_test)
# Оцениваем полиномиальную модель на тестовых данных
poly_r2 = r2_score(y_test, y_poly_pred_test)
print(f"\nПолиномиальная регрессия (degree={degree}, на тесте): R^2 = {poly_r2:.3f}")
# Полиномиальная регрессия (degree=2, на тесте): R^2 = 0.639Если `include_bias=True` (по умолчанию), то к генерируемым признакам добавляется столбец из единиц. Этот столбец соответствует члену `x⁰ = 1` и позволяет модели линейной регрессии в дальнейшем оценить свободный член (`β₀`) как коэффициент при этом столбце. Но реализация `sklearn.linear_model.LinearRegression` по умолчанию сама вычисляет свободный член (`β₀`) — за это отвечает её параметр `fit_intercept=True`.
Чтобы избежать избыточности (когда и `PolynomialFeatures`, и `LinearRegression` пытаются добавить/вычислить свободный член), рекомендуется использовать одну из двух комбинаций:
Мы будем придерживаться первого, более распространенного подхода.
Чтобы избежать избыточности (когда и `PolynomialFeatures`, и `LinearRegression` пытаются добавить/вычислить свободный член), рекомендуется использовать одну из двух комбинаций:
- `PolynomialFeatures(include_bias=False)` + `LinearRegression(fit_intercept=True)` (Самый частый и рекомендуемый способ)** +
- `PolynomialFeatures(include_bias=True)` + `LinearRegression(fit_intercept=False)`.
Мы будем придерживаться первого, более распространенного подхода.
И так же сделаем визуализацию:
plt.figure(figsize=(12, 7))
plt.scatter(X['horsepower'], y, alpha=0.6, label='Все данные')
# Предсказания полиномиальной модели для диапазона X_plot
y_poly_plot = poly_reg_pipeline.predict(X_plot)
plt.plot(X_plot, y_poly_plot, color='green', linewidth=3, label=f'Полиномиальная регрессия (degree={degree}, R^2={poly_r2:.3f})')
# Можно добавить и линейную для сравнения
plt.plot(X_plot, y_lin_plot, color='red', linewidth=1, linestyle='--', label=f'Линейная регрессия (R^2={lin_r2:.3f})')
plt.title('Сравнение линейной и полиномиальной регрессии второй степени')
plt.xlabel('Мощность (Horsepower)')
plt.ylabel('Расход топлива (MPG)')
plt.legend()
plt.grid(True)
plt.show()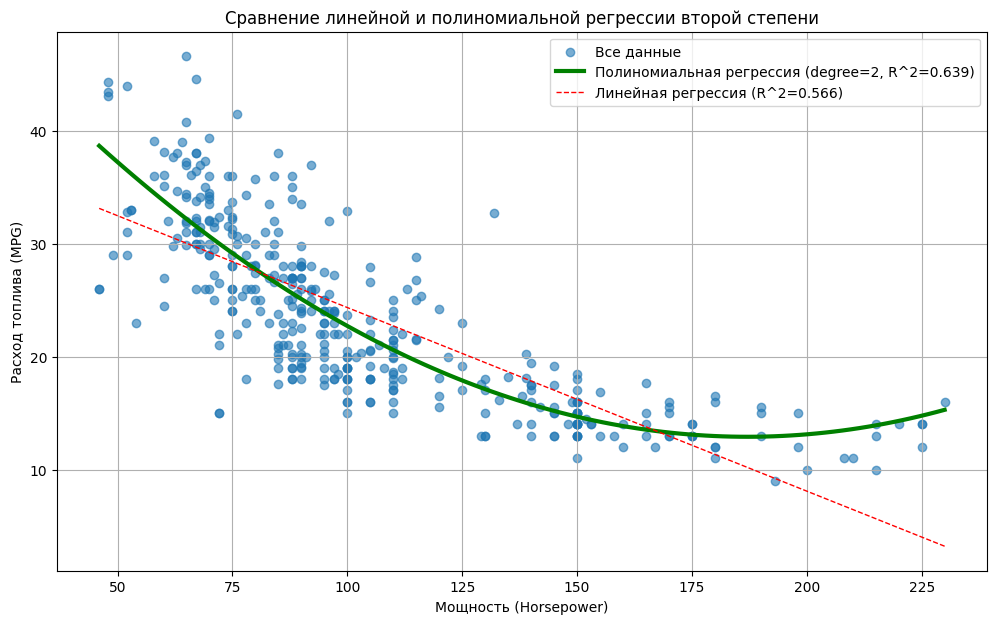
Зеленая параболическая кривая лучше следует за точками данных, чем красная прямая. R² получается выше, чем у линейной модели.
Прогнозирование новых значений
Как предсказать MPG для автомобиля с мощностью, например, 110 л.с.? Не забываем применить ту же трансформацию, что и при обучении полиномиальной модели.
# Новое значение мощности, для которого хотим сделать прогноз
hp_new_value = 110
hp_new = pd.DataFrame({'horsepower': [hp_new_value]})
# Предсказание простой линейной моделью
mpg_pred_lin = lin_reg.predict(hp_new)
print(f"\nПрогноз MPG (линейная модель) для мощности {hp_new_value} л.с.: {mpg_pred_lin[0]:.2f}")
# Прогноз MPG (линейная модель) для мощности 110 л.с.: 22.72
# Предсказание полиномиальной моделью
mpg_pred_poly = poly_reg_pipeline.predict(hp_new)
print(f"Прогноз MPG (полиномиальная модель, degree={degree}) для мощности {hp_new_value} л.с.: {mpg_pred_poly[0]:.2f}")
# Прогноз MPG (полиномиальная модель, degree=2) для мощности 110 л.с.: 20.59Два разных прогноза. Полиномиальная модель, даст прогноз, который лучше соответствует наблюдаемой кривой зависимости.
Переобучение и выбор степени полинома
Гибкость полиномиальной регрессии может обернуться против нас. Слишком простая модель (низкая степень полинома) не уловит тренд, а слишком сложная (высокая степень) начнет подстраиваться под случайный шум в обучающих данных.
Недообучение (underfitting)
Это происходит, когда модель слишком проста для описания основной закономерности. В нашем случае, как мы уже видели, базовая линейная регрессия является примером недообучения для зависимости MPG от Horsepower. Она не может уловить криволинейный характер падения расхода топлива с ростом мощности. Такая модель имеет высокое смещение (bias) — она делает систематическую ошибку, неверно предполагая линейность.
Признаки недообучения:
- Плохое качество модели как на обучающих, так и на новых (тестовых) данных.
- Линия или кривая регрессии явно не следует за общим трендом точек данных.
Переобучение (overfitting)
Это обратная проблема: модель слишком сложна. При использовании высокой степени полинома (например, 10 или 15) модель становится настолько гибкой, что начинает подстраиваться не только под основной тренд, но и под случайные флуктуации и шум, присутствующие именно в обучающей выборке. Такая модель будет показывать отличные результаты на данных, на которых обучалась, но будет плохо обобщаться на новые, ранее невиданные данные (т.е. плохо работать на тестовой выборке). Она имеет высокую вариативность (variance) — небольшие изменения в обучающих данных могут привести к сильным изменениям формы кривой.
Признаки переобучения:
- Отличное качество на обучающих данных.
- Значительно худшее качество на новых (тестовых) данных.
- Кривая регрессии становится очень "извилистой", совершает резкие колебания, пытаясь пройти как можно ближе к каждой точке обучающей выборки. Зачастую такая кривая выглядит неправдоподобно с точки зрения предметной области.
Визуализация проблемы
Давайте посмотрим, как выглядят модели с разными степенями полинома на наших данных MPG vs Horsepower. Мы также рассчитаем качество моделей (R²) на обучающей и тестовой выборках для каждой степени.
X_plot = np.linspace(X['horsepower'].min(), X['horsepower'].max(), 200).reshape(-1, 1)
X_plot_df = pd.DataFrame(X_plot, columns=['horsepower'])
degrees = [1, 2, 15] # Степени для сравнения: недообучение, баланс, переобучение
colors = ['red', 'green', 'purple']
labels = ["Степень 1 - недообучение",
"Степень 2 - баланс?",
"Степень 15 - явное переобучение"]
train_r2s = []
test_r2s = []
plt.figure(figsize=(14, 8))
plt.scatter(X_train['horsepower'], y_train, alpha=0.6, label='Обучающие данные')
plt.scatter(X_test['horsepower'], y_test, alpha=0.8, marker='^', label='Тестовые данные')
for i, degree in enumerate(degrees):
model = make_pipeline(
PolynomialFeatures(degree, include_bias=False),
LinearRegression()
)
model.fit(X_train, y_train)
# Предсказания для графика
y_plot_pred = model.predict(X_plot_df)
# Предсказания для оценки R^2
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
# Расчет R^2
train_r2 = r2_score(y_train, y_train_pred)
test_r2 = r2_score(y_test, y_test_pred)
train_r2s.append(train_r2)
test_r2s.append(test_r2)
# Рисуем кривую
plt.plot(X_plot, y_plot_pred, color=colors[i], linewidth=2.5,
label=f"{labels[i]} (Test R^2: {test_r2:.2f})")
plt.title('Недообучение, сбалансированная модель и переобучение (MPG vs Horsepower)')
plt.xlabel('Мощность (Horsepower)')
plt.ylabel('Расход топлива (MPG)')
plt.legend(loc='upper right')
plt.grid(True)
# Ограничим ось Y для наглядности, иначе кривая степени 15 может улететь
plt.ylim(data['mpg'].min() - 5, data['mpg'].max() + 10)
plt.show()
# Выведем R^2 для сравнения
print("\nСравнение R^2 для разных степеней:")
for i, degree in enumerate(degrees):
print(f"Степень {degree}: Train R^2 = {train_r2s[i]:.2f}, Test R^2 = {test_r2s[i]:.2f}")
# Сравнение R^2 для разных степеней:
# Степень 1: Train R^2 = 0.61, Test R^2 = 0.57
# Степень 2: Train R^2 = 0.70, Test R^2 = 0.64
# Степень 15: Train R^2 = 0.42, Test R^2 = 0.44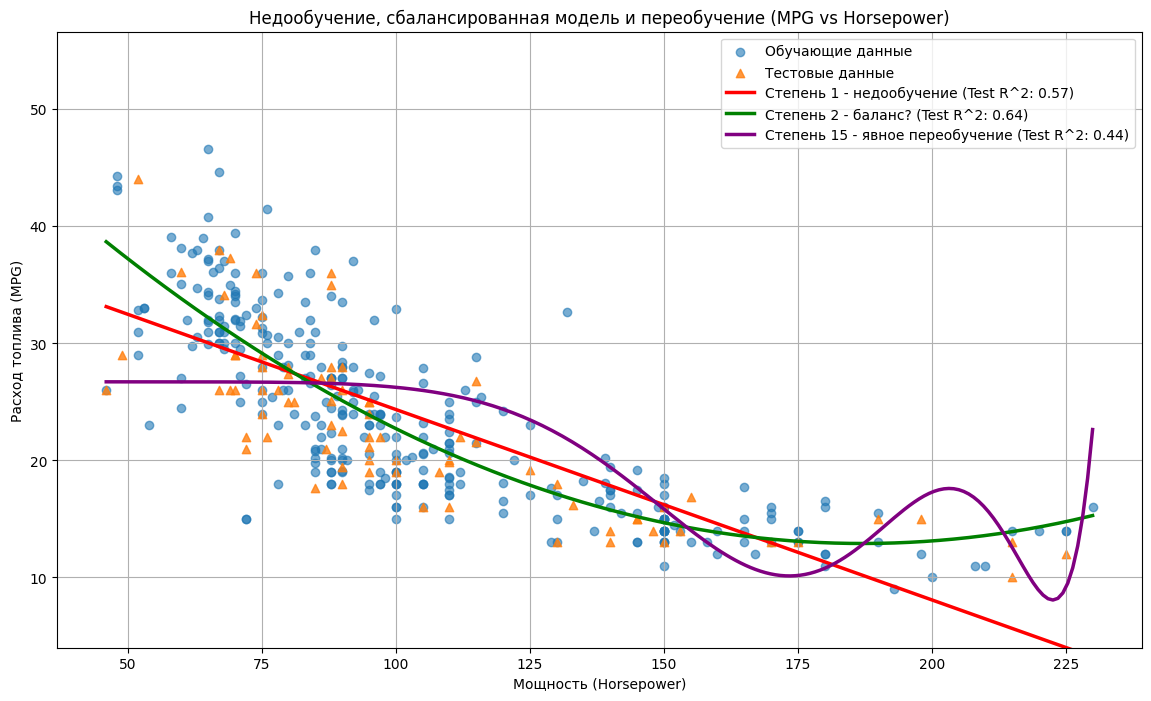
- Красная линия (cтепень 1): прямая, плохо описывает данные, R² относительно низкий.
- Зеленая кривая (степень 2): парабола, гораздо лучше следует тренду, R² выше, чем у линейной модели.
- Фиолетовая кривая (степень 15): очень извилистая. Она показывает значительно худший результат (низкий R²) как на обучающей, так и на тестовой выборке по сравнению со степенью 2, что указывает на сильное переобучение и деградацию модели.
Компромисс смещения и вариативности (bias-variance trade-off)
Проблемы недо- и переобучения — это проявление фундаментального компромисса в машинном обучении:
Наша цель — найти "золотую середину": модель с достаточно низкой степенью, чтобы не переобучаться (контролировать вариативность), но достаточно высокой, чтобы уловить основной тренд (контролировать смещение). В нашем примере, степень 2 выглядит как хороший кандидат.
- У простых моделей будет высокое смещение (bias), низкая вариативность (variance). Модель систематически ошибается, но устойчива к изменениям в данных.
- У сложных моделей будет низкое смещение и высокая вариативность. Модель хорошо подстраивается под обучающие данные, но очень чувствительна к их особенностям и шуму.
Наша цель — найти "золотую середину": модель с достаточно низкой степенью, чтобы не переобучаться (контролировать вариативность), но достаточно высокой, чтобы уловить основной тренд (контролировать смещение). В нашем примере, степень 2 выглядит как хороший кандидат.
Как выбрать оптимальную степень полинома?
Как мы только что и сделали, можно построить графики для нескольких степеней и выбрать ту, которая хорошо описывает зависимость, но не выглядит слишком "извилистой" или неправдоподобной. Можно ещё построить график зависимости ошибки на обучающей и тестовой выборках от степени полинома. Ошибка на обучении будет падать с ростом степени, а ошибка на тесте сначала упадет, а потом начнет расти (точка начала роста — признак переобучения). Ищем "локоть" или минимум на кривой тестовой ошибки.
# --- Построение графика R² от степени полинома ---
degrees_to_test = range(1, 16) # Протестируем степени от 1 до 15
train_scores = []
test_scores = []
for degree in degrees_to_test:
model = make_pipeline(
PolynomialFeatures(degree, include_bias=False),
LinearRegression()
)
model.fit(X_train, y_train)
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
train_scores.append(r2_score(y_train, y_train_pred))
test_scores.append(r2_score(y_test, y_test_pred))
plt.figure(figsize=(10, 6))
plt.plot(degrees_to_test, train_scores, 'bo-', label='Train R²')
plt.plot(degrees_to_test, test_scores, 'ro-', label='Test R²')
plt.xlabel('Степень полинома')
plt.ylabel('R²')
plt.title('R² на обучающей и тестовой выборках vs степень полинома')
plt.legend()
plt.grid(True)
# Отметим максимум на тестовой кривой
best_degree_idx = np.argmax(test_scores)
best_degree = degrees_to_test[best_degree_idx]
plt.axvline(best_degree, linestyle='--', color='gray', label=f'Оптимальная степень ≈ {best_degree}')
plt.legend()
plt.ylim(min(train_scores + test_scores) - 0.1, 1.1) # Настроить масштаб оси Y
plt.xticks(degrees_to_test[::2]) # Показать не все тики на оси X
plt.show()
print(f"\nМаксимальный R² на тесте (R²={test_scores[best_degree_idx]:.2f}) достигается при степени {best_degree}")
# Максимальный R² на тесте (R²=0.65) достигается при степени 5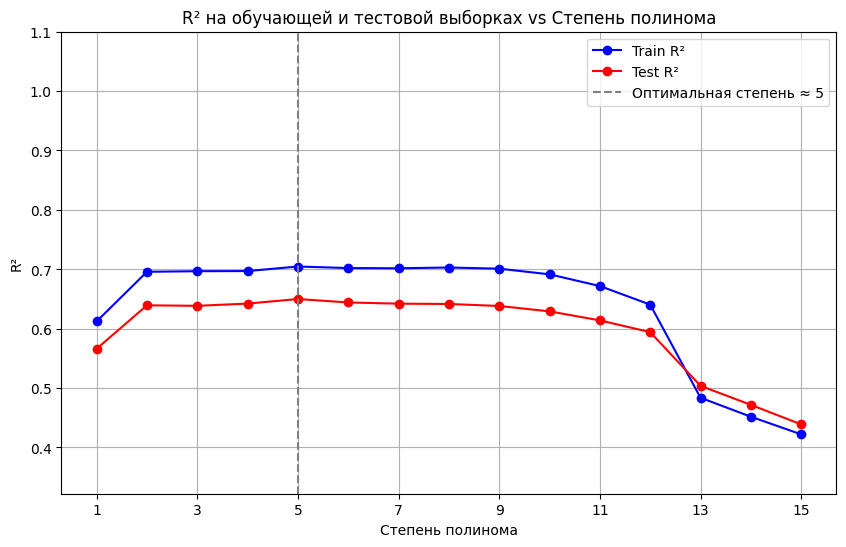
R² на тесте растет вначале, но затем достигает максимума (в нашем случае, при степени 5) и после этого начинает немного снижаться. Точка максимума указывает на оптимальную сложность модели. Снижение после максимума — явный признак того, что модель становится слишком сложной и начинает переобучаться, теряя качество на новых данных.
Что ещё можно улучшить?
Что ещё можно улучшить?
- Использовать кросс-валидацию. Данные многократно разбиваются на обучающие и валидационные фолды, модель обучается и оценивается несколько раз для каждой степени. Результаты усредняются. Scikit-learn имеет встроенные инструменты для кросс-валидации (например, cross_val_score или GridSearchCV для поиска оптимальной степени).
- Принцип простоты/экономности (бритва Оккама). Если две модели с разными степенями дают примерно одинаковое качество на валидационных/тестовых данных, выбираем более простую модель.
- Регуляризация. Вместо того чтобы подбирать степень, можно использовать полином достаточно высокой степени, но добавить к функции потерь штраф за большие коэффициенты модели (L1 - Lasso, L2 - Ridge). Это "сглаживает" кривую и борется с переобучением, не требуя явного выбора оптимальной степени (хотя требует подбора параметра регуляризации). Это особенно полезно, когда признаков много и есть взаимодействия.
Заключение: изгибаем линии с умом
Как и любой другой метод, полиномиальная регрессия имеет свои достоинства и недостатки. Понимание их поможет вам решить, подходит ли этот инструмент для вашей конкретной задачи. Давайте кратко суммируем её сильные стороны:
- Моделирование нелинейности. Главное преимущество — способность эффективно описывать криволинейные зависимости и сложные взаимодействия между признаками.
- Гибкость. Изменяя степень полинома (n), можно контролировать сложность модели, адаптируя её под данные.
- Относительная простота реализации. Основана на понятной линейной регрессии, легко реализуется с помощью стандартных библиотек (как Scikit-learn).
- Интерпретируемость (частичная). Для полиномов невысоких степеней (например, 2 или 3) и при небольшом числе признаков можно попытаться интерпретировать влияние каждого члена (линейного, квадратичного, взаимодействия) на результат.
Однако, как и любой мощный инструмент, она требует осторожного обращения. Важно помнить о недостатках:
- Риск переобучения. Это, пожалуй, самый главный недостаток и основная опасность. С увеличением степени полинома модель легко подстраивается под шум в обучающих данных, теряя способность к обобщению на новые данные.
- Сложность выбора оптимальной степени. Найти степень, которая достаточно гибка, но не переобучена, — может быть нетривиальной задачей, требующей дополнительных шагов (визуальный анализ, валидация на тестовой выборке, кросс-валидация, построение кривых обучения).
- Чувствительность к выбросам. Как и обычная линейная регрессия (основанная на минимизации квадратов ошибок), полиномиальная регрессия может быть сильно подвержена влиянию выбросов в данных. Одна или несколько аномальных точек могут сильно исказить форму кривой, особенно при высоких степенях.
- Плохая экстраполяция. Полиномиальные модели могут вести себя очень непредсказуемо за пределами диапазона значений X, на которых они обучались. Кривая высокой степени может резко уходить вверх или вниз, давая совершенно нереалистичные прогнозы.
- Проблема мультиколлинеарности. При высоких степенях полинома признаки x, x², x³, ... (а также взаимодействия) могут сильно коррелировать друг с другом. Это может приводить к неустойчивости оценок коэффициентов β и затруднять их интерпретацию (хотя на точность предсказаний это может влиять меньше, особенно если используется регуляризация).
- Снижение интерпретируемости с ростом степени. Если для степени 2 еще можно говорить о "параболическом эффекте", то интерпретировать значение коэффициента при x⁷ или сложном взаимодействии типа x₁²*x₂³ становится практически невозможно. Модель превращается в "черный ящик".
Итого: полиномиальная регрессия — полезный и относительно простой инструмент для добавления нелинейности в регрессионные модели. Освоив полиномиальную регрессию, вы можете двигаться дальше к изучению регуляризации (Ridge, Lasso, ElasticNet) для еще более эффективной борьбы с переобучением в полиномиальных моделях, или исследовать другие методы моделирования нелинейности, такие как деревья решений, ансамблевые методы, нейронные сети и пр.
