«Ящик с усами», он же боксплот или диаграмма размаха — одна из самых полезных, но и самых непонятных для новичков визуализаций в анализе данных. На первый взгляд, это просто странный прямоугольник с линиями. На самом деле, он дает исчерпывающее представление о распределении данных, помогает находить выбросы и сравнивать группы между собой.
В этом руководстве мы разберем анатомию боксплота от и до. Вы не просто научитесь его «читать», но и поймете, какая математика стоит за каждой его частью, и, конечно, научитесь строить и интерпретировать такие графики на Python с помощью matplotlib, seaborn и pandas.
Что такое «ящик с усами»?
Представьте, что у вас есть набор данных. Вы можете посчитать среднее, медиану или моду, но этих мер центральной тенденции часто недостаточно. Нужно понимать, насколько данные изменчивы, как они разбросаны, есть ли в них аномалии.
Боксплот — это стандартизированный способ визуализировать распределение на основе сводки из пяти ключевых чисел:
- Минимум
- Первый квартиль (Q1)
- Медиана (Q2)
- Третий квартиль (Q3)
- Максимум
Он наглядно показывает симметричность данных, их плотность, наличие перекосов и выбросов. В сравнении с гистограммой или графиком плотности, боксплот может показаться менее интуитивным, но он несет в себе гораздо больше концентрированной информации.
Анатомия боксплота
Давайте препарируем наш «ящик» и разберем каждую его часть
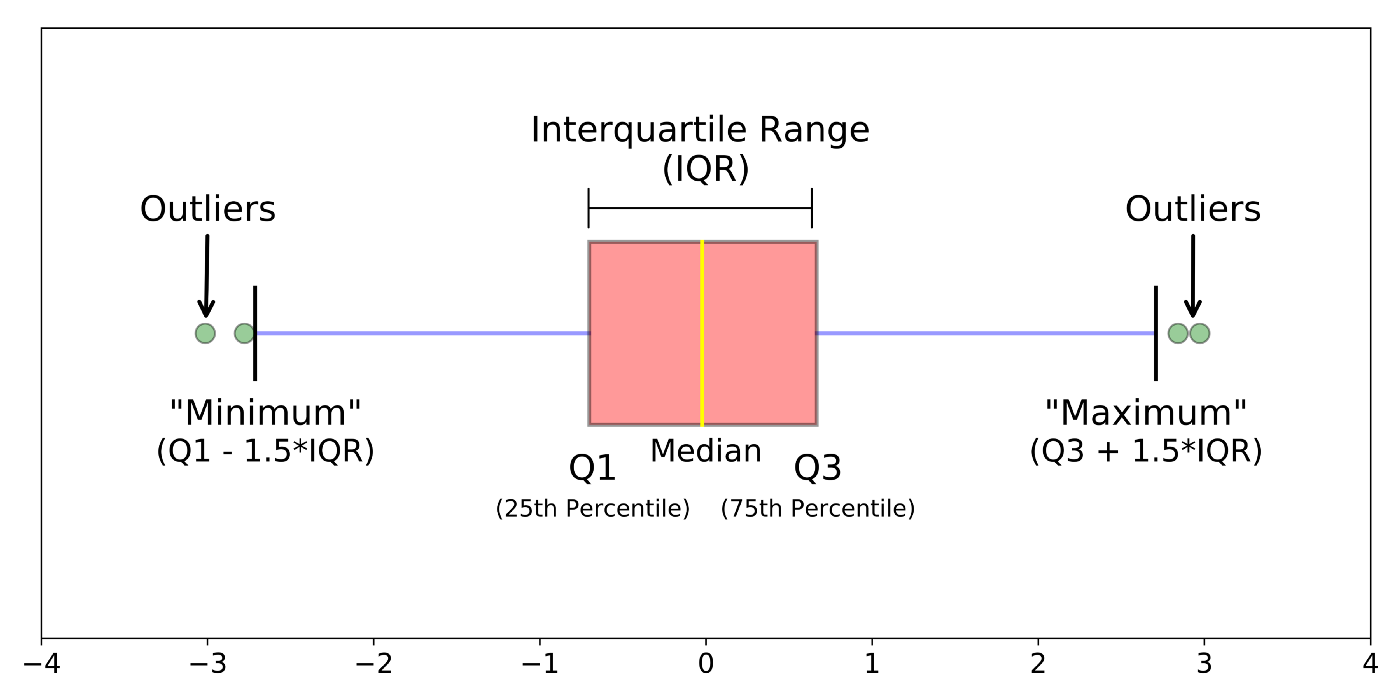
- Медиана (Q2 / 50-й процентиль): Линия, разделяющая «ящик» на две части. Это значение, которое делит отсортированный набор данных ровно пополам. 50% всех точек данных находятся ниже этой отметки, а 50% — выше.
- Первый квартиль (Q1 / 25-й процентиль): Нижняя граница «ящика». Это значение отсекает нижние 25% данных.
- Третий квартиль (Q3 / 75-й процентиль): Верхняя граница «ящика». Это значение отсекает верхние 25% данных (или, что то же самое, 75% всех данных находятся ниже этой отметки).
- Межквартильный размах (IQR — Interquartile Range): Это «высота» самого ящика, которая вычисляется как
Q3 - Q1. В этом диапазоне лежит центральная половина (50%) всех ваших данных. IQR — это ключевая мера разброса, устойчивая к выбросам.
[!INFO] Квартили делят ваши данные на четыре равные части. Процентили делят их на 100 частей. Таким образом, Q1 — это 25-й процентиль, медиана (Q2) — 50-й, а Q3 — 75-й.
Теперь разберемся с «усами» и точками за их пределами.
- «Усы» (whiskers): Линии, отходящие от ящика. Они показывают весь разброс данных, за исключением выбросов. Их границы часто определяются по стандартному методу Тьюки:
- Верхний ус (Максимум):
Q3 + 1.5 * IQR. Это верхняя граница «нормального» диапазона данных. - Нижний ус (Минимум):
Q1 - 1.5 * IQR. Это нижняя граница «нормального» диапазона.
- Верхний ус (Максимум):
- Выбросы (outliers): Любые точки данных, которые лежат за пределами «усов». Это аномально высокие или аномально низкие значения, которые требуют особого внимания.
Связь боксплота с нормальным распределением
Чтобы глубже понять суть боксплота, полезно посмотреть, как он выглядит для идеального, эталонного случая — нормального распределения.
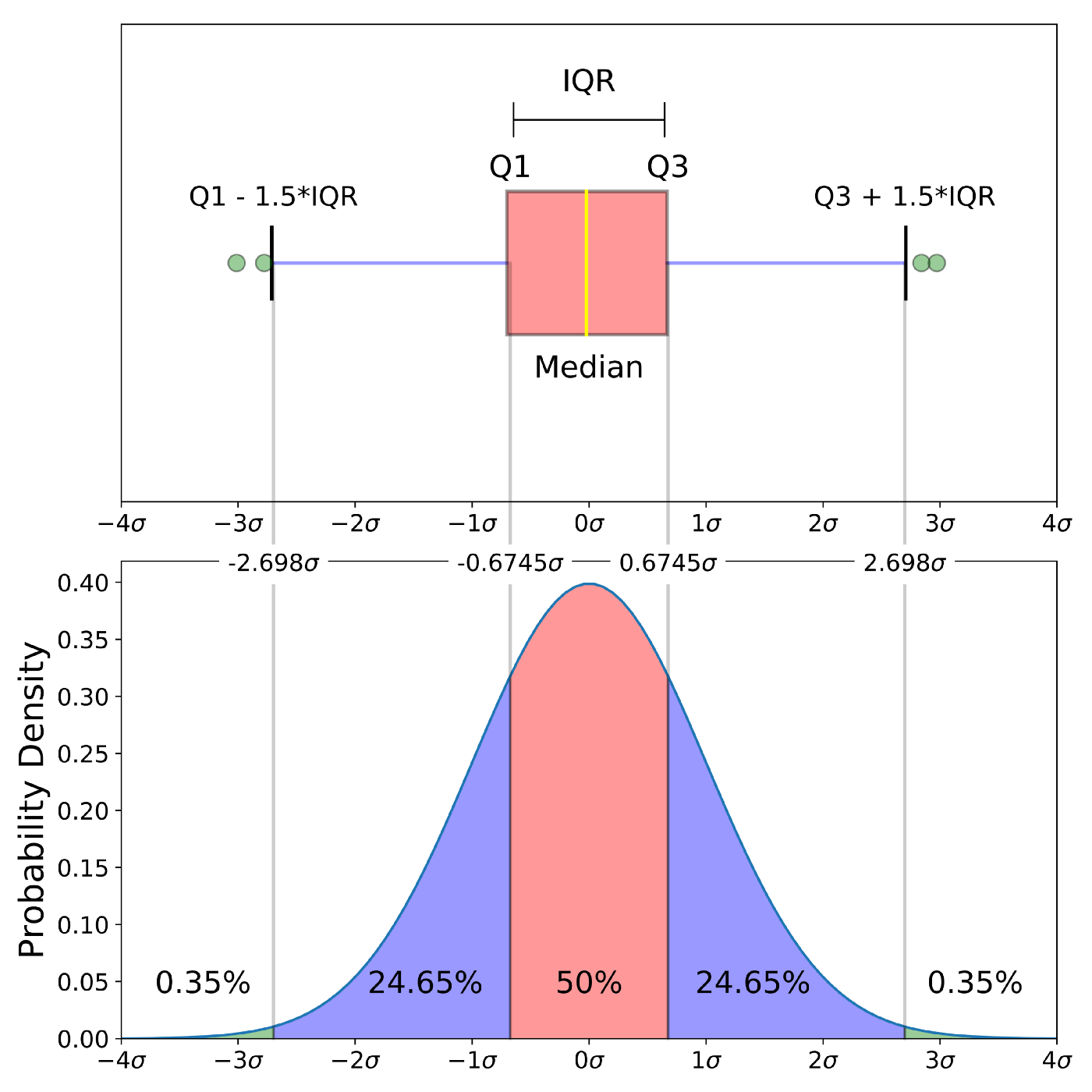
На рисунке выше показано, как части боксплота соответствуют областям под кривой плотности вероятности (Probability Density Function, PDF) для нормального распределения.
Что такое плотность вероятности (PDF)?
Не пугайтесь, сейчас все станет просто. PDF — это функция, которая описывает вероятность того, что случайная величина примет определенное значение. Для непрерывных данных (как в нашем случае), вероятность попадания в конкретный диапазон равна площади под кривой PDF в этом диапазоне.
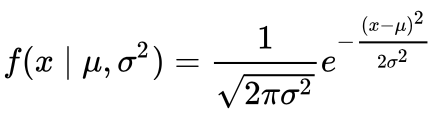
Для стандартного нормального распределения (где среднее μ = 0 и стандартное отклонение σ = 1), формула упрощается.
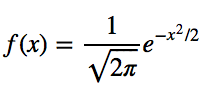
Давайте построим этот знаменитый «колокол» с помощью Python.
# Импортируем необходимые библиотеки
from scipy.integrate import quad
import numpy as np
import matplotlib.pyplot as plt
# Генерируем данные для оси X
x = np.linspace(-4, 4, num = 100)
# Рассчитываем PDF для стандартного нормального распределения
constant = 1.0 / np.sqrt(2 * np.pi)
pdf_normal_distribution = constant * np.exp((-x**2) / 2.0)
# Строим график
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, pdf_normal_distribution)
ax.set_ylim(0)
ax.set_title('График плотности вероятности нормального распределения', size = 16)
ax.set_ylabel('Плотность вероятности', size = 14)
plt.show()
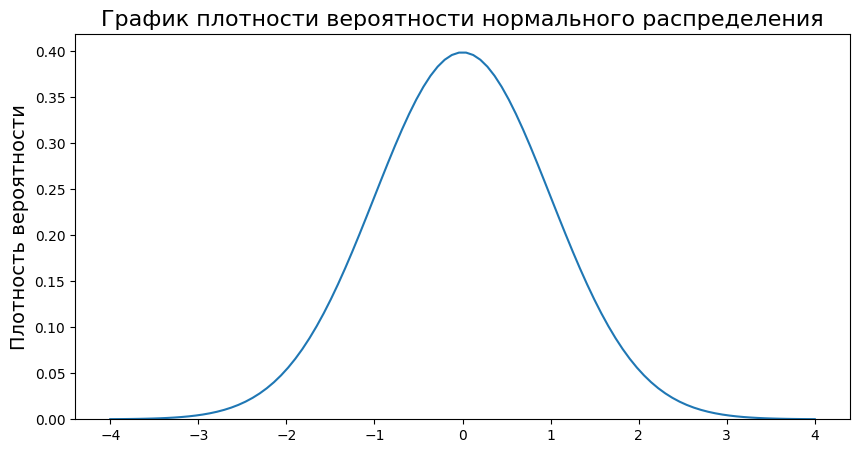
Теперь самое интересное. Мы можем посчитать, какая доля данных лежит в межквартильном диапазоне. Для нормального распределения Q1 и Q3 находятся на расстоянии примерно 0.6745 стандартных отклонений от среднего. Чтобы найти вероятность, нам нужно взять интеграл (то есть посчитать площадь под кривой) от -0.6745 до 0.6745.
К счастью, Python сделает это за нас.
# Функция, описывающая нашу кривую
def normal_probability_density(x):
constant = 1.0 / np.sqrt(2 * np.pi)
return(constant * np.exp((-x**2) / 2.0))
# Считаем интеграл для межквартильного размаха
# quad возвращает результат и оценку погрешности, нам нужен только результат
iqr_prob, _ = quad(normal_probability_density, -0.6745, 0.6745, limit = 1000)
print(f"Вероятность попадания в межквартильный размах: {iqr_prob:.4f}")
# Вывод: Вероятность попадания в межквартильный размах: 0.5000
Результат — 0.5, что идеально соответствует определению IQR, который содержит 50% данных.
Аналогично, границы «усов» для нормального распределения (±2.698 стандартных отклонений) охватывают примерно 99.3% данных. Оставшиеся 0.7% — это и есть теоретические выбросы.
[!TIP] Ключевой вывод: Боксплот — это не просто рисунок. Его структура математически связана с распределением вероятностей. Понимание этой связи позволяет извлекать из графика максимум информации.
Теперь, когда мы буквально по косточкам разобрали теоретическую часть с помощью Python, перейдем к практике.
Построение и интерпретация графиков на реальных данных
Теория — это хорошо, но в реальной жизни данные редко бывают идеально нормальными. Давайте применим наши знания на настоящем датасете. Мы будем использовать распространённый "Висконсинский диагностический набор данных по раку молочной железы".
Наша задача — с помощью боксплотов проанализировать взаимосвязь между категориальным признаком (диагноз: злокачественная или доброкачественная опухоль) и непрерывным признаком (например, средняя площадь опухоли area_mean).
Загрузка данных
Первым делом загрузим данные в DataFrame.
import pandas as pd
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['diagnosis'] = data.target
print("\nРаспределение по диагнозам:")
print(df['diagnosis'].value_counts())
Распределение по диагнозам:
diagnosis
1 357
0 212
Name: count, dtype: int64Построение графиков
В Python есть много библиотек для визуализации. Рассмотрим три самых популярных способа построить боксплот для сравнения групп.
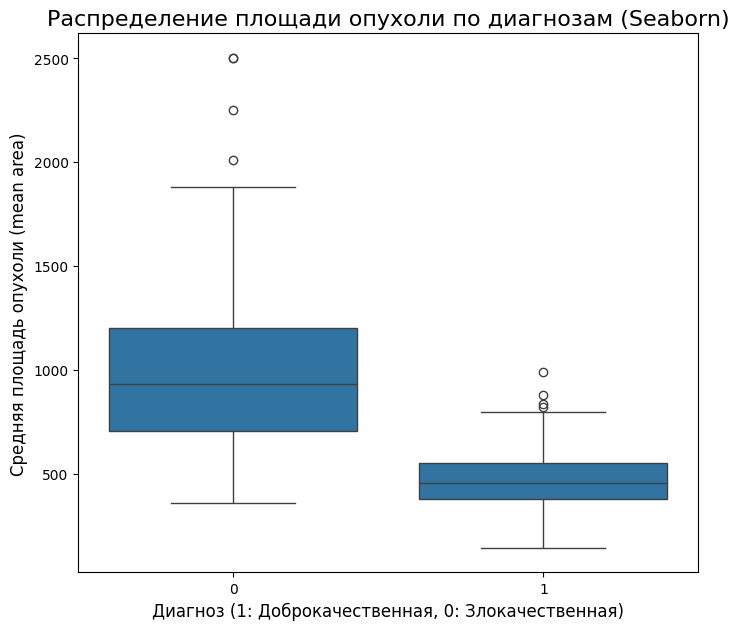
1. Seaborn: быстро и красиво
Seaborn — это высокоуровневая библиотека, которая позволяет строить красивые статистические графики с минимальными усилиями. Это, пожалуй, самый простой и рекомендуемый способ для подобных задач.
import seaborn as sns
plt.figure(figsize=(8, 7))
sns.boxplot(x='diagnosis', y='mean area', data=df)
plt.title('Распределение площади опухоли по диагнозам (Seaborn)', fontsize=16)
plt.xlabel('Диагноз (1: Доброкачественная, 0: Злокачественная)', fontsize=12)
plt.ylabel('Средняя площадь опухоли (mean area)', fontsize=12)
plt.show()
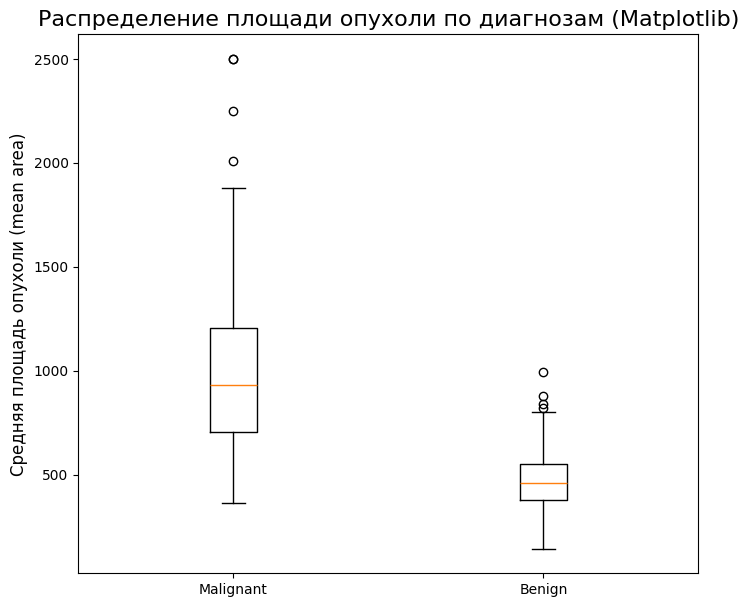
2. Matplotlib: полный контроль
Matplotlib — это базовая библиотека, которая лежит в основе seaborn. Она дает абсолютный контроль над каждым элементом графика, но требует чуть больше кода.
import matplotlib.pyplot as plt
# Сначала нужно подготовить данные: разделить их на две выборки
malignant = df[df['diagnosis'] == 0]['mean area']
benign = df[df['diagnosis'] == 1]['mean area']
fig, ax = plt.subplots(figsize=(8, 7))
# Matplotlib принимает данные в виде списка списков/массивов
ax.boxplot([malignant, benign], labels=['Malignant', 'Benign'])
ax.set_title('Распределение площади опухоли по диагнозам (Matplotlib)', fontsize=16)
ax.set_ylabel('Средняя площадь опухоли (mean area)', fontsize=12)
plt.show()
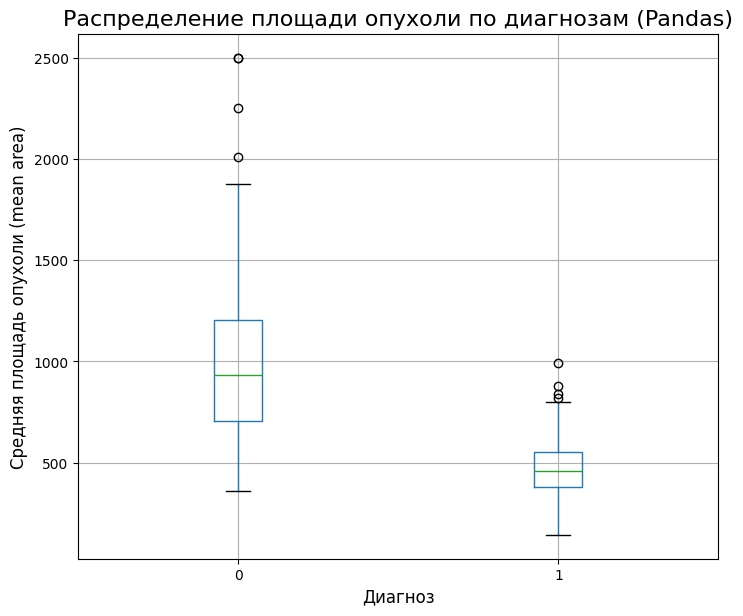
3. Pandas: встроенный метод
У pandas есть свои встроенные методы для быстрой визуализации, которые являются оберткой над matplotlib. Это удобно для экспресс-анализа прямо из DataFrame.
fig, ax = plt.subplots(figsize=(8, 7))
df.boxplot(column='mean area', by='diagnosis', ax=ax)
# Pandas создает свой заголовок, который лучше заменить или убрать
plt.suptitle('') # Убираем автоматический заголовок
plt.title('Распределение площади опухоли по диагнозам (Pandas)', fontsize=16)
plt.xlabel('Диагноз', fontsize=12)
plt.ylabel('Средняя площадь опухоли (mean area)', fontsize=12)
plt.show()
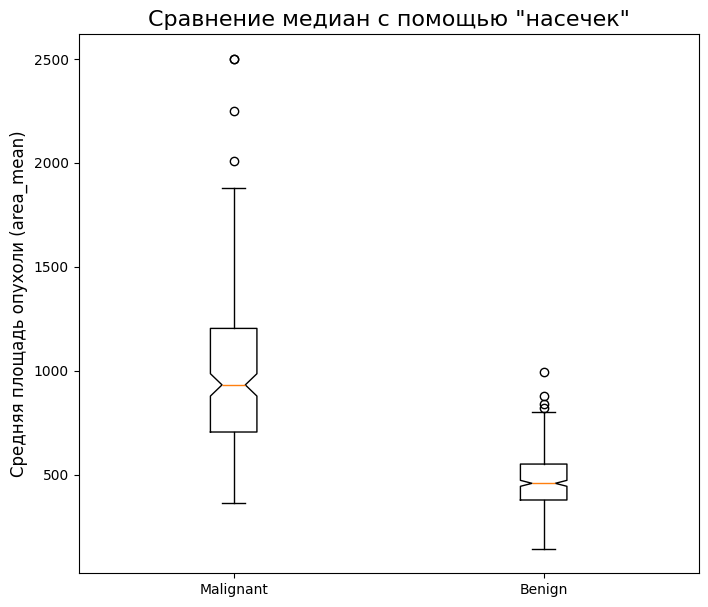
Боксплоты с «насечками» (Notched Boxplots)
Иногда вы хотите не просто посмотреть на распределения, а сравнить их медианы с определенной долей уверенности. Для этого существуют боксплоты с «насечками» (notch). Эти насечки представляют собой доверительный интервал (по умолчанию 95%) вокруг медианы.
[!TIP] Простое правило: если насечки двух боксплотов не пересекаются, это является статистически значимым свидетельством того, что их медианы действительно различаются.
# Используем код для Matplotlib, добавив один параметр: notch=True
malignant = df[df['diagnosis'] == 0]['mean area']
benign = df[df['diagnosis'] == 1]['mean area']
fig, ax = plt.subplots(figsize=(8, 7))
ax.boxplot([malignant, benign], labels=['Malignant', 'Benign'], notch=True) # Вот и вся магия
ax.set_title('Сравнение медиан с помощью "насечек"', fontsize=16)
ax.set_ylabel('Средняя площадь опухоли (area_mean)', fontsize=12)
plt.show()
Понравился материал?
Ваша поддержка — это энергия для новых статей и проектов. Спасибо, что читаете!
Финальная интерпретация
Давайте посмотрим на последний график и сделаем выводы, которые можно получить буквально за несколько секунд, взглянув на боксплот.
- Сравнение медиан: Медианное значение
area_meanдля злокачественных опухолей (Malignant) значительно выше, чем для доброкачественных (Benign). Это логично и ожидаемо. График с насечками подтверждает, что это различие статистически значимо (насечки не пересекаются). - Разброс данных (IQR): «Ящик» для злокачественных опухолей гораздо шире и расположен выше. Это говорит о большем разбросе значений площади. Можно сделать гипотезу, что злокачественные опухоли более гетерогенны по своим размерам.
- Асимметрия и выбросы: В группе
Malignantесть несколько верхних выбросов. Это пациенты с аномально большой площадью опухоли, которые могут требовать отдельного изучения. В группеBenignвыбросов меньше, что указывает на более стабильные и предсказуемые размеры доброкачественных новообразований. - Общий диапазон: «Усы» злокачественных опухолей простираются гораздо дальше, что еще раз подчеркивает их большую изменчивость.
[!NOTE] Важно помнить, что
matplotlibи другие библиотеки вычисляют квартили и границы усов непосредственно из данных, а не из какой-то теоретической модели распределения. Поэтому внешний вид вашего боксплота всегда будет зависеть от конкретной выборки, ее размера и реального распределения.
